Question

【题目】如图，椭圆C： 经过点P（1， ），离心率e= ，直线l的方程为x=4．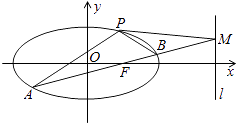

（1）求椭圆C的方程；
（2）AB是经过右焦点F的任一弦（不经过点P），设直线AB与直线l相交于点M，记PA，PB，PM的斜率分别为k1 ， k2 ， k3 ． 问：是否存在常数λ，使得k1+k2=λk3？若存在，求λ的值；若不存在，说明理由．

Answer 1

【答案】
（1）解：椭圆C： 经过点P （1， ），可得 ①

由离心率e= 得 = ，即a=2c，则b2=3c2②，代入①解得c=1，a=2，b=

故椭圆的方程为

（2）解：方法一：由题意可设AB的斜率为k，则直线AB的方程为y=k（x﹣1）③

代入椭圆方程 并整理得（4k2+3）x2﹣8k2x+4k2﹣12=0

设A（x1，y1），B（x2，y2），

x1+x2= ， ④

在方程③中，令x=4得，M的坐标为（4，3k），

从而 ， ， =k﹣

注意到A，F，B共线，则有k=kAF=kBF，即有 = =k

所以k1+k2= + = + ﹣ （ + ）

=2k﹣ × ⑤

④代入⑤得k1+k2=2k﹣ × 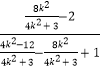=2k﹣1

又k3=k﹣ ，所以k1+k2=2k3

故存在常数λ=2符合题意

方法二：设B（x0，y0）（x0≠1），则直线FB的方程为

令x=4，求得M（4， ）

从而直线PM的斜率为k3= ，

联立 ，得A（ ， ），

则直线PA的斜率k1= ，直线PB的斜率为k2=

所以k1+k2= + =2× =2k3，

故存在常数λ=2符合题意

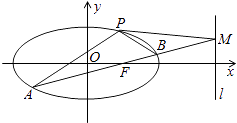
【解析】（1）由题意将点P （1， ）代入椭圆的方程，得到 ，再由离心率为e= ，将a，b用c表示出来代入方程，解得c，从而解得a，b，即可得到椭圆的标准方程；（2）方法一：可先设出直线AB的方程为y=k（x﹣1），代入椭圆的方程并整理成关于x的一元二次方程，设A（x1 ， y1），B（x2 ， y2），利用根与系数的关系求得x1+x2= ， ，再求点M的坐标，分别表示出k1 ， k2 ， k3 ． 比较k1+k2=λk3即可求得参数的值；方法二：设B（x0 ， y0）（x0≠1），以之表示出直线FB的方程为 ，由此方程求得M的坐标，再与椭圆方程联立，求得A的坐标，由此表示出k1 ， k2 ， k3 ． 比较k1+k2=λk3即可求得参数的值
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：，焦点在y轴：．