Question

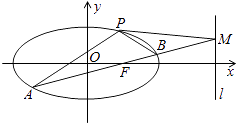
【题目】已知⊙的半径为，圆心的坐标为，其中．，为该圆的两条切线，为坐标原点，，为切点，在第一象限，在第四象限．

（）若时，求切线，的斜率．

（）若时，求外接圆的标准方程．

（）当点在轴上运动时，将表示成的函数，并求函数的最小值．

Answer 1

【答案】(1)斜率为，为．

(2).

(3).

【解析】分析：（1）设出切线方程，根据圆心到切线的距离等于半径可得斜率．（2）由题意外接圆的圆心在轴上，设为．结合平面几何的有关知识可得圆心为，半径为，进而可得圆的方程．（3）结合（2）中的结论可得点的坐标，进而得向量的坐标，然后根据数量积的结果和函数的单调性可得所求．

详解：（）当时，圆的方程为．

由题意得过点的圆的切线的斜率存在，设其方程为，

由直线和圆相切得，

解得．

所以斜率为，为．

（）由题意外接圆的圆心在轴上，设为，

由平面几何知识得，

可得，．

又，

即，

解得．

所以外接圆圆心为，半径为．

所以圆．

（）由（）知，

可得，，

所以，，，

所以．

所以，

易得函数在区间上单调递减，

所以当时，取得最小值为．