题目内容
在等腰△ABC中，M是底边BC的中点，AM=3，BC=8，则
•
=________．
-7
分析：由已知条件在三角形中利用勾股定理求得边长，求出角的函数值进而求得∠BAC的余弦值，然后由向量的数量级的定义的答案．
解答：
解：由题意可知：在直角三角形ABM中，AM=3，BM=4，
由勾股定理可得AB=
，由于△ABC为等腰三角形，
所以AC=AB=5，，在直角三角形ABM中cos∠BAM=
，
∴cos∠BAC=cos2∠BAM=2cos2∠BAM-1=
∴
=
=
故答案为：-7
点评：本题为向量的数量级的运算，利用三角函数知识求解夹角的余弦值是解决问题的关键，属中档题．
分析：由已知条件在三角形中利用勾股定理求得边长，求出角的函数值进而求得∠BAC的余弦值，然后由向量的数量级的定义的答案．
解答：
解：由题意可知：在直角三角形ABM中，AM=3，BM=4，由勾股定理可得AB=
，由于△ABC为等腰三角形，所以AC=AB=5，，在直角三角形ABM中cos∠BAM=
，∴cos∠BAC=cos2∠BAM=2cos2∠BAM-1=
∴
==故答案为：-7
点评：本题为向量的数量级的运算，利用三角函数知识求解夹角的余弦值是解决问题的关键，属中档题．
练习册系列答案
阅读快车系列答案
相关题目
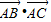AD，过E作MN∥BC，分别交AB、AC于M、N．以MN为折痕将△AMN折起到△A′MN的位置，使二面角A′－MN－D为60°，求证：平面A′MN⊥平面A′BC．
= ．