题目内容
已知点P在直线x+2y-1=0上,点Q在直线x+2y+3=0上,PQ中点为N(x,y),且y>x+2,则 的取值范围为 .
的取值范围为 .
【答案】分析:首先由直线x+2y-1=0与直线x+2y+3=0是平行线,得出PQ的中点M(x,y)满足的直线方程;再根据y>x+2对应的平面区域进一步限定M的范围;最后结合 的几何意义求出其范围.
的几何意义求出其范围.
解答: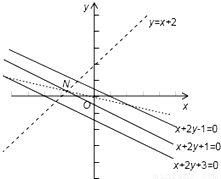 解:根据题意作图如下
解:根据题意作图如下
因为PQ中点为N,则点M的坐标满足方程x+2y+1=0,
又y>x+2,则点N在直线y=x+2的左上部,
且由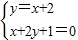 得 N(
得 N(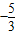 ,
, ),则kON=-
),则kON=- ,并且直线x+2y+1=0的斜率k=-
,并且直线x+2y+1=0的斜率k=- ,
,
而 可视为点N与原点O连线的斜率,
可视为点N与原点O连线的斜率,
故- <
< <-
<- .
.
点评:本题考查数形结合的思想方法.
 的几何意义求出其范围.
的几何意义求出其范围.解答:
 解:根据题意作图如下
解:根据题意作图如下因为PQ中点为N,则点M的坐标满足方程x+2y+1=0,
又y>x+2,则点N在直线y=x+2的左上部,
且由
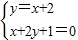 得 N(
得 N(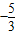 ,
, ),则kON=-
),则kON=- ,并且直线x+2y+1=0的斜率k=-
,并且直线x+2y+1=0的斜率k=- ,
,而
 可视为点N与原点O连线的斜率,
可视为点N与原点O连线的斜率,故-
 <
< <-
<- .
.点评:本题考查数形结合的思想方法.

练习册系列答案
相关题目
已知点P在直线x+2y-1=0上,点Q在直线x+2y+3=0上,PQ的中点为M(x0,y0),且y0>x0+2,则
的取值范围是( )
| y0 |
| x0 |
A、(-
| ||||
B、(-
| ||||
C、[-
| ||||
D、[-
|