题目内容
3.在平面直角坐标系xoy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆C的右焦点F作两条互相垂直的弦EF与MN,当直线EF斜率为0时,|EF|+|MN|=7.(1)求椭圆C的方程;
(2)求|EF|+|MN|的取值范围.
分析 (1)由题意知e=$\frac{c}{a}$=$\frac{1}{2}$,MN=7-2a,再由点(c,$\frac{7-4c}{2}$)在椭圆上,能求出椭圆的方程.
(2)当两条弦中一条斜率为0时,另一条弦的斜率不存在时,|EF|+|MN|=7;当两弦斜率均存在且不为0时,设直线EF的方程为y=k(x-1),直线MN的方程为y=-$\frac{1}{k}$(x-1).由此能求出|EF|+|MN|,从而能求出其取值范围.
解答 解:(1)由题意知,e=$\frac{c}{a}$=$\frac{1}{2}$,|MN|=7-2a,
所以a2=4c2,b2=3c2,…2分
因为点(c,$\frac{7-4c}{2}$)在椭圆上,
即$\frac{{c}^{2}}{{4c}^{2}}$+$\frac{{(\frac{7-4c}{2})}^{2}}{{3c}^{2}}$=1,解得:c=1.
所以椭圆的方程为:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)①当两条弦中一条斜率为0时,另一条弦的斜率不存在,
由题意知|EF|+|MN|=7,
②当两弦斜率均存在且不为0时,
设直线EF的方程为y=k(x-1),
则直线MN的方程为:y=-$\frac{1}{k}$(x-1),
将直线EF的方程代入椭圆方程中,
并整理得(3+4k2)x2-8k2x+4k2-12=0,
∴x1=$\frac{{4k}^{2}-6\sqrt{{k}^{2}+1}}{3+{4k}^{2}}$,x2=$\frac{{4k}^{2}+6\sqrt{{k}^{2}+1}}{3+{4k}^{2}}$,
∴|EF|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\frac{12{(k}^{2}+1)}{3+{4k}^{2}}$,同理,|MN|=$\frac{12{(k}^{2}+1)}{{3k}^{2}+4}$,
∴|EF|+|MN|=$\frac{8{4{(k}^{2}+1)}^{2}}{(3+{4k}^{2})({3k}^{2}+4)}$,
令t=k2+1,则t>1,3+4k2=4t-1,3k2+4=3t+1,
设f(t)=$\frac{(4t-1)(3t+1)}{{t}^{2}}$=-${(\frac{1}{t}-\frac{1}{2})}^{2}$+$\frac{49}{4}$,
∵t>1,∴$\frac{1}{t}$∈(0,1),
∴f(t)∈(12,$\frac{49}{4}$),
∴|EF|+|MN|=$\frac{84}{f(t)}$∈[$\frac{48}{7}$,7].
综合①与②可知,AB+CD的取值范围是[$\frac{48}{7}$,7].
点评 本题考查椭圆的方程的求法,考查两条线段和的取值范围的求法,解题时要认真审题,注意分类讨论思想的合理运用.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (1,+∞) | B. | (0,1) | C. | (0,+∞) | D. | ∅ |
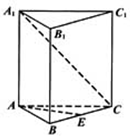 如图,已知正三棱柱ABC-A1B1C1的各棱长均相等,E是BC的中点,点F在侧棱CC1上,且CC1=4CF
如图,已知正三棱柱ABC-A1B1C1的各棱长均相等,E是BC的中点,点F在侧棱CC1上,且CC1=4CF 如图,设A,B分比为椭圆E$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点,P是椭圆E上不同于A,B的一动点,点F是椭圆E的右焦点,直线l是椭圆E的右准线,若直线AP与直线:x=a和l分别相较于C,Q两点,FQ与直线BC交于M.
如图,设A,B分比为椭圆E$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点,P是椭圆E上不同于A,B的一动点,点F是椭圆E的右焦点,直线l是椭圆E的右准线,若直线AP与直线:x=a和l分别相较于C,Q两点,FQ与直线BC交于M. 某校团委会组织该校高中一年级某班以小组为单位利用周末时间进行了一次社会实践活动,且每个小组有5名同学,在实践活动结束后,学校团委会对该班的所有同学都进行了测评,该班的A、B两个小组所有同学所得分数(百分制)的茎叶图如图所示,其中B组一同学的分数已被污损,但知道B组学生的平均分比A组学生的平均分高1分.
某校团委会组织该校高中一年级某班以小组为单位利用周末时间进行了一次社会实践活动,且每个小组有5名同学,在实践活动结束后,学校团委会对该班的所有同学都进行了测评,该班的A、B两个小组所有同学所得分数(百分制)的茎叶图如图所示,其中B组一同学的分数已被污损,但知道B组学生的平均分比A组学生的平均分高1分. 如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等边三角形,AB=4,AA1=5,点M是BB1中点
如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等边三角形,AB=4,AA1=5,点M是BB1中点