题目内容
已知函数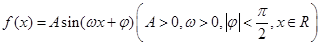 图象的一部分如图所示.
图象的一部分如图所示.
(1)求函数 的解析式;
的解析式;
(2)当 时,求函数
时,求函数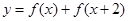 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值.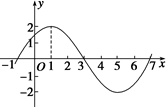
(1)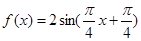 ;(2)
;(2)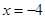 时,
时, ,
,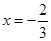 时,
时,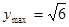 .
.
解析试题分析:(1)从图象中可得振幅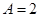 ,
,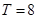 ,从而可知
,从而可知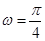 ,再由图象过点
,再由图象过点 可知
可知 ,结合条件中
,结合条件中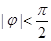 即可得
即可得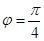 ,从而
,从而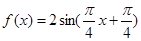 ;(2)利用诱导公式及辅助角公式对
;(2)利用诱导公式及辅助角公式对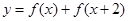 进行恒等变形:
进行恒等变形: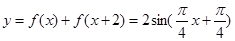
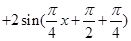
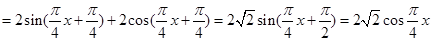 ,
,
再由余弦函数的性质结合条件可知:由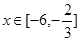 可知
可知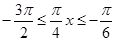 ,
,
因此当 时,即
时,即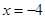 时,
时, ,当
,当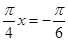 时,即
时,即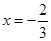 时,
时,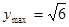 .
.
试题解析:(1)由图象知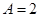 ,
,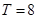 ,∵
,∵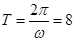 ,∴
,∴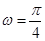 ,
,
又∵图象过点 ,∴
,∴ ,∵
,∵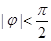 ,∴
,∴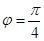 ,∴
,∴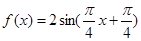 ;(6分)
;(6分)
(2)由(1)可知,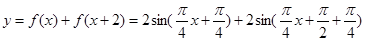
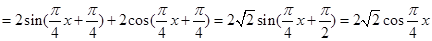 ,
,
∵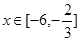 ,∴
,∴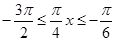 ,
,
∴当 时,即
时,即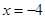 时,
时, ,当
,当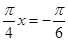 时,即
时,即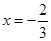 时,
时,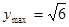 .
.
考点:1.三角函数的图象和性质;2.三角函数的最值.

练习册系列答案
相关题目
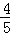 ,α为第三象限角.
,α为第三象限角.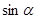 ,
, 的值;
的值;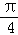 ),tan2α的值.
),tan2α的值. ,
, ,若函数
,若函数 .
. 的最小正周期;
的最小正周期;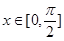 ,求
,求 值;
值; ,求
,求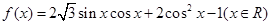 ,
,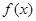 的最小正周期及在区间
的最小正周期及在区间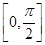 上的最大值和最小值;
上的最大值和最小值;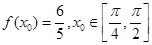 ,求
,求 的值.
的值. <j<0)图象上的任意两点,且角j的终边经过点P(l,-
<j<0)图象上的任意两点,且角j的终边经过点P(l,- ),若|f(x1)-f(x2)|=4时,|x1-x2|的最小值为
),若|f(x1)-f(x2)|=4时,|x1-x2|的最小值为 .
.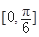 时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围. .
. ;
; 是第三象限角,且
是第三象限角,且 ,求
,求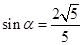 ,
,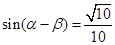 ,且
,且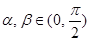 .求:
.求: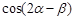 的值;(2)
的值;(2) 的值.
的值.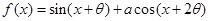 ,其中
,其中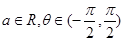
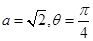 时,求
时,求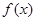 在区间
在区间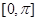 上的最大值与最小值;
上的最大值与最小值;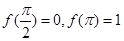 ,求
,求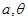 的值.
的值. =________.
=________.