题目内容
12.已知角θ的终边经过点P(3,-4).(1)求sinθ,cosθ和tanθ的值;
(2)求$\frac{cos(3π-θ)+cos(\frac{3π}{2}+θ)}{sin(\frac{π}{2}-θ)+tan(π+θ)}$的值.
分析 (1)由题意可得 x=3,y=-4,r=5,根据三角函数的定义可得sinθ,cosθ和tanθ的值.
(2)利用诱导公式化简所求,结合(1)结论即可计算得解.
解答 (本题满分为12分)
解:(1)因为角θ的终边经过点P(3,-4),
所以x=3,y=-4,
所以 $r=\sqrt{{3^2}+(-4{)^2}}=5$,…(1分)
所以 $sinθ=\frac{y}{r}=-\frac{4}{5}$,…(3分)
$cosθ=\frac{x}{r}=\frac{3}{5}$,…(5分)
$tanθ=\frac{y}{x}=-\frac{4}{3}$.…(7分)
(2)因为 cos(3π-θ)=-cosθ,…(8分)
$cos(\frac{3π}{2}+θ)=sinθ$,…(9分)
$sin(\frac{π}{2}-θ)=cosθ$,…(10分)
tan(π+θ)=tanθ,…(11分)
所以$\frac{{cos(3π-θ)+cos(\frac{3π}{2}+θ)}}{{sin(\frac{π}{2}-θ)+tan(π+θ)}}=\frac{-cosθ+sinθ}{cosθ+tanθ}$…(12分)
=$\frac{{-\frac{3}{5}-\frac{4}{5}}}{{\frac{3}{5}-\frac{4}{3}}}=\frac{21}{11}$. …(14分)
点评 本题考查任意角的三角函数的定义,两点间的距离公式,诱导公式的应用,求出x、y、r 的值,是解题的突破口,属于基础题.

练习册系列答案
相关题目
3.己知函数 $f(x)=\frac{x-1}{x}$(其中$x∈[{\frac{1}{2},2}]$)的值域为( )
| A. | $[{-1,\frac{1}{2}}]$ | B. | [-1,2] | C. | $[{\frac{1}{2},2}]$ | D. | $[{\frac{1}{2},1}]$ |
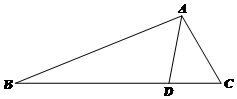 如图,在△ABC中,D是BC上的点,AC=3,CD=2,AD=$\sqrt{7}$,sinB=$\frac{\sqrt{7}}{7}$.
如图,在△ABC中,D是BC上的点,AC=3,CD=2,AD=$\sqrt{7}$,sinB=$\frac{\sqrt{7}}{7}$.