题目内容
已知抛物线C:x2=2py(p>0)的焦点是F,准线是l,经过C上两点A、B分别作C的切线l1、l2.
(1)设点A(x1,
),求直线l1的方程(用x1和p表示);
(2)设l1与l2的交点E在l上,若△ABE面积S的最小值是4,求C的方程.
(1)设点A(x1,
| x12 |
| 2p |
(2)设l1与l2的交点E在l上,若△ABE面积S的最小值是4,求C的方程.
考点:利用导数研究曲线上某点切线方程,轨迹方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)由题意,求导y′|x=x1=
x1,从而写出直线l1的方程;
(2)同理写出直线l2的方程为2x2x-2py-
=0,联立可得
从而可推得p2=-x1x2,可知直线AB过点F,从而当AB∥l时,面积最小,从而求出p,得到C的方程.
| 1 |
| p |
(2)同理写出直线l2的方程为2x2x-2py-
| x | 2 2 |
|
解答:
解:(1)∵x2=2py(p>0),
∴y=
x2,y′=
x,
则y′|x=x1=
x1,
则直线l1的方程为y-
=
x1(x-x1),
即2x1x-2py-
=0.
(2)由题意,
直线l2的方程为2x2x-2py-
=0,
设点E的坐标为(x,y),则
则可推出x=
=
=
,
则p2=-x1x2,
则直线AB的方程为y-
=
(x-x1),
且
-
=
(0-x1),
故直线AB恒过点F,
则当AB∥l时,面积最小,
即
p•2p=4,
解得,p=2,
故C的方程为x2=4y.
∴y=
| 1 |
| 2p |
| 1 |
| p |
则y′|x=x1=
| 1 |
| p |
则直线l1的方程为y-
| x12 |
| 2p |
| 1 |
| p |
即2x1x-2py-
| x | 2 1 |
(2)由题意,
直线l2的方程为2x2x-2py-
| x | 2 2 |
设点E的坐标为(x,y),则
|
则可推出x=
| ||
| 2x1 |
| ||
| 2x2 |
| x1+x2 |
| 2 |
则p2=-x1x2,
则直线AB的方程为y-
| x12 |
| 2p |
| x1+x2 |
| 2p |
且
| p |
| 2 |
| x12 |
| 2p |
| x1+x2 |
| 2p |
故直线AB恒过点F,
则当AB∥l时,面积最小,
即
| 1 |
| 2 |
解得,p=2,
故C的方程为x2=4y.
点评:本题考查了圆锥曲线中线与曲线的位置关系,属于中档题.

练习册系列答案
相关题目
380°角是第几象限角( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
P是椭圆
+
=1上一点,F1、F2分别是椭圆的左、右焦点,若|PF1|•|PF2|=12,则∠F1PF2的大小为( )
| x2 |
| 16 |
| y2 |
| 9 |
| A、30° | B、60° |
| C、120° | D、150° |
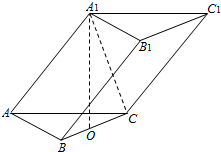 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=