题目内容
如图，等边三角形ABC的面积等于1，连接这个三角形各边的中点得到一个小三角形，又连接这个小三角形各边的中点得到一个更小的三角形，如此无限继续下去，求所有这些三角形的面积的和．
【答案】分析：先设第n个三角形的面积为an根据三角形面积公式得出a1，a2，a3，发现数列{an}为等比数列，进而求出前n项和的极限，即可得到答案．
解答：解：设第n个三角形的面积为an，则a1=
=
，a2=
=
，
a3=
=
∴数列{an}为首项为
，公比为
的等比数列．
所有这些三角形的面积的和为
（a1+a2+a3+…an）=
=
点评：本题主要考查等比数列求和公式的应用．属基础题．
解答：解：设第n个三角形的面积为an，则a1=
=，a2==，a3=
=∴数列{an}为首项为
，公比为的等比数列．所有这些三角形的面积的和为
（a1+a2+a3+…an）==点评：本题主要考查等比数列求和公式的应用．属基础题．
练习册系列答案
相关题目
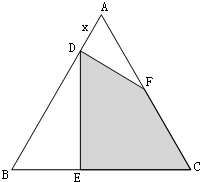
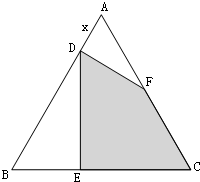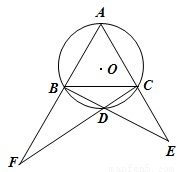
如图，等边三角形ABC的边长为6，在AB上截取AD，过D点作DF⊥AB，交AC于点F，过D点作DE⊥BC，交BC于点E．设AD=x，四边形DECF的面积为y．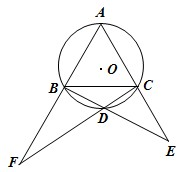
（2012•盐城二模）选修4-1：几何证明选讲：
选修4-1：几何证明选讲：
