题目内容

（2012•盐城二模）选修4-1：几何证明选讲：
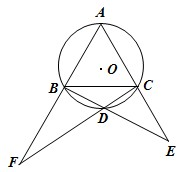
如图，等边三角形ABC内接于圆O，D为劣弧BC上一点，连接BD，CD并延长分别交AC，AB的延长线于点E，F．
求证：CE•BF=BC2．
分析：证明BC2=BF•CE，即证
BF
BC
=
BC
CE
，证明△CBE∽△BFC即可．
解答：证明：因为三角形ABC内接于圆O，且∠BAC=60°，所以∠BDC=120°，
∴∠DBC+∠DCB=60°
又∠BFC+∠DCB=60°，所以∠DBC=∠BFC
同理，∠DCB=∠CEB，
所以△CBE∽△BFC
所以
BF
BC
=
BC
CE
，即BC2=BF•CE
点评：本题考查与圆有关的比例线段，考查三角形的相似，证明三角形相似是关键．
练习册系列答案
相关题目
（2012•盐城二模）若命题“?x∈R，x2-ax+a≥0”为真命题，则实数a的取值范围是
[0，4]
[0，4]
．
（2012•盐城二模）已知集合P={-1，m}，Q={x|-1＜x＜
34
}，若P∩Q≠∅，则整数m=
0
0
．
（2012•盐城二模）设△ABC的内角A，B，C的对边长分别为a，b，c，且b2=
1
2
ac．
（1）求证：cosB≥
3
4
；
（2）若cos（A-C）+cosB=1，求角B的大小．
（2012•盐城二模）已知函数f1(x)=e|x-2a+1|，f2(x)=e|x-a|+1，x∈R．
（1）若a=2，求f（x）=f1（x）+f2（x）在x∈[2，3]上的最小值；
（2）若x∈[a，+∞）时，f2（x）≥f1（x），求a的取值范围；
（3）求函数g(x)=
f1(x)+f2(x)
2
-
|f1(x)-f2(x)|
2
在x∈[1，6]上的最小值．
（2012•盐城二模）设f（x）是定义在R上的可导函数，且满足f（x）+xf′（x）＞0．则不等式f(
x+1
)＞
x-1
f(
x2-1
)的解集为
{x|1≤x＜2}
{x|1≤x＜2}
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网