题目内容
13.求函数y=$\sqrt{{x}^{2}-4x+5}$+$\sqrt{{x}^{2}+2x+5}$的最小值.分析 运用配方,可知函数表示x轴上一点P(x,0)到定点A(2,1),B(-1,-2)的距离,由于A,B分别在x轴的两边,连接AB,由两点之间线段最短,计算即可得到最小值.
解答 解:函数y=$\sqrt{{x}^{2}-4x+5}$+$\sqrt{{x}^{2}+2x+5}$
=$\sqrt{(x-2)^{2}+1}$+$\sqrt{(x+1)^{2}+4}$
=$\sqrt{(x-2)^{2}+(0-1)^{2}}$+$\sqrt{(x+1)^{2}+(0+2)^{2}}$,
表示x轴上一点P(x,0)到定点A(2,1),B(-1,-2)的距离,
由于A,B分别在x轴的两边,连接AB,
可得|AB|=$\sqrt{(2+1)^{2}+(1+2)^{2}}$=3$\sqrt{2}$.
则函数y=$\sqrt{{x}^{2}-4x+5}$+$\sqrt{{x}^{2}+2x+5}$的最小值为3$\sqrt{2}$.
点评 本题考查函数最值的求法,注意运用转化思想,考查运算能力,属于中档题.

练习册系列答案
相关题目
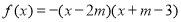 (其中
(其中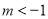 ),
),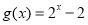 .
.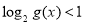 ”是真命题,求
”是真命题,求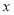 的取值范围;
的取值范围;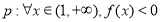 或
或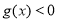 ;命题
;命题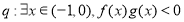 ,若
,若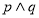 是真命题,求
是真命题,求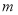 的取值范围.
的取值范围. ”是“函数
”是“函数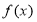 是奇函数”的充要条件
是奇函数”的充要条件 ,则
,则 ”的否命题是“若
”的否命题是“若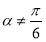 ,则
,则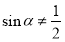 ”
”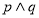 为假命题,则
为假命题,则 均为假命题
均为假命题 ,
, ,则
,则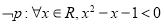
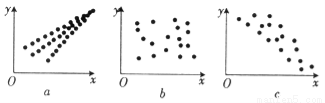
 为正相关,
为正相关,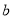 为负相关,
为负相关,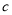 为不相关
为不相关 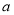 为负相关,
为负相关,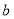 为不相关,
为不相关,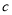 为正相关
为正相关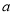 为负相关,
为负相关,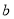 为正相关,
为正相关,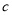 为不相关
为不相关 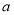 为正相关,
为正相关,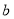 为不相关,
为不相关,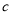 为负相关
为负相关