题目内容
数列{an}是等差数列,a1=f(a+1),a2=3,a3=f(a-1),其中a为实数,f(x)=x2-4x+5.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an}单调递增,设bn=2nan,求数列{bn}的前n项和.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an}单调递增,设bn=2nan,求数列{bn}的前n项和.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:分析:(Ⅰ)利用等差数列中,a2是a1与a3的等差中项则有2a2=a1+a3,列出关于a的方程,并求出a,再代入等差数列通项公式中求出通项公式an;
(Ⅱ)把数列{an}的通项公式代入bn=2nan,利用错位相减法求数列{bn}的前n项和.
(Ⅱ)把数列{an}的通项公式代入bn=2nan,利用错位相减法求数列{bn}的前n项和.
解答:
解:(Ⅰ)∵数列{an}是等差数列,∴2a2=a1+a3
又∵a1=f(a+1)=(a+1)2-4(a+1)+5,a3=f(a-1)=(a-1)2-4(a-1)+5,a2=3,
∴(a+1)2-4(a+1)+5+(a-1)2-4(a-1)+5=6,解得a=1或a=3.
当a=1时,a1=f(2)=1,公差d=2,∴通项公式an=a1+(n-1)d=2n-1,
当a=3时,a1=f(4)=5,公差d=-2,∴通项公式an=a1+(n-1)d=7-2n.
故当a=1时,通项公式an=2n-1,
当a=3时,通项公式an=7-2n;
(Ⅱ)∵数列{an}单调递增,∴an=2n-1,
则bn=2nan=(2n-1)2n.
设数列{bn}的前n项和为Sn,
∴Sn=1•21+3•22+…+(2n-1)•2n,
2Sn=1•22+3•23+…+(2n-1)•2n+1,
作差得-Sn=2+2•22+2•23+…+2•2n-(2n-1)•2n+1
=2+2×
-(2n-1)•2n+1=2+2n+2-8-(2n-1)•2n+1=(-2n+3)•2n+1-6.
∴Sn=(2n-3)•2n+1+6.
又∵a1=f(a+1)=(a+1)2-4(a+1)+5,a3=f(a-1)=(a-1)2-4(a-1)+5,a2=3,
∴(a+1)2-4(a+1)+5+(a-1)2-4(a-1)+5=6,解得a=1或a=3.
当a=1时,a1=f(2)=1,公差d=2,∴通项公式an=a1+(n-1)d=2n-1,
当a=3时,a1=f(4)=5,公差d=-2,∴通项公式an=a1+(n-1)d=7-2n.
故当a=1时,通项公式an=2n-1,
当a=3时,通项公式an=7-2n;
(Ⅱ)∵数列{an}单调递增,∴an=2n-1,
则bn=2nan=(2n-1)2n.
设数列{bn}的前n项和为Sn,
∴Sn=1•21+3•22+…+(2n-1)•2n,
2Sn=1•22+3•23+…+(2n-1)•2n+1,
作差得-Sn=2+2•22+2•23+…+2•2n-(2n-1)•2n+1
=2+2×
| 4(1-2n-1) |
| 1-2 |
∴Sn=(2n-3)•2n+1+6.
点评:本题主要考查等差数列的等差中项这个性质,以及函数的分类讨论思想,考查了错位相减法求数列的和,是中档题.

练习册系列答案
相关题目
在△ABC中,三内角A,B,C的对边分别为a,b,c,面积为S,若S+a2=(b+c)2,则cosA等于( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
双曲线
-
=1的右焦点到抛物线y2=4x的准线的距离为( )
| x2 |
| 4 |
| y2 |
| 12 |
| A、5 | B、4 | C、3 | D、2 |
已知函数f(x)=cosx(sinx+cosx)+ksin(x+
)sin(x-
).
(1)当k=2时,求函数f(x)在区间(0,
)内的值域;
(2)tanα=
时,f(α)=
,求k的值.
| π |
| 4 |
| π |
| 4 |
(1)当k=2时,求函数f(x)在区间(0,
| π |
| 2 |
(2)tanα=
| 1 |
| 2 |
| 3 |
| 2 |
已知向量
,
满足|
|=1,
⊥
,则
-2
在
方向上的投影为( )
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| A、1 | ||||
B、
| ||||
| C、-1 | ||||
D、
|
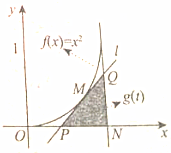 如图,抛物线f(x)=x2(0<x<1)在点M(t,f(t))处的切线为l,l与x轴和直线x=1分别交于点P,Q,直线x=1与x轴的交点为N,设△PQN的面积为g(t)
如图,抛物线f(x)=x2(0<x<1)在点M(t,f(t))处的切线为l,l与x轴和直线x=1分别交于点P,Q,直线x=1与x轴的交点为N,设△PQN的面积为g(t)