题目内容
(2013•丽水一模)已知数列{an}的首项a1=1,其前n项和Sn=n2•an(n∈N*),则a9=
.
| 1 |
| 45 |
| 1 |
| 45 |
分析:由Sn=n2•an(n∈N*)①,得Sn-1=(n-1)2•an-1(n≥2)②,两式相减可得递推式,整理变为
=
,利用累乘法即可求得a9.
| an |
| an-1 |
| n-1 |
| n+1 |
解答:解:由Sn=n2•an(n∈N*)①,得Sn-1=(n-1)2•an-1(n≥2)②,
①-②得an=n2•an-(n-1)2•an-1,即(n2-1)an-(n-1)2an-1=0,
又a1=1,所以
=
,
所以a9=a1•
×
×
×…×
=1×
×
×
×…×
=
×
=
,
故答案为:
.
①-②得an=n2•an-(n-1)2•an-1,即(n2-1)an-(n-1)2an-1=0,
又a1=1,所以
| an |
| an-1 |
| n-1 |
| n+1 |
所以a9=a1•
| a2 |
| a1 |
| a3 |
| a2 |
| a4 |
| a3 |
| a9 |
| a8 |
| 1 |
| 3 |
| 2 |
| 4 |
| 3 |
| 5 |
| 8 |
| 10 |
| 2 |
| 9 |
| 1 |
| 10 |
| 1 |
| 45 |
故答案为:
| 1 |
| 45 |
点评:本题考查数列求和及通项公式,考查数列的递推公式,若数列{an}满足
=f(n),则可考虑用累乘法求an,且an=a1•
•
…
(n≥2),注意检验n=1时情形.
| an+1 |
| an |
| a2 |
| a1 |
| a3 |
| a2 |
| an |
| an-1 |

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
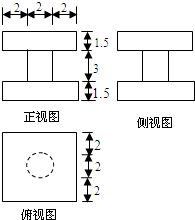 (2013•丽水一模)某几何体的三视图如图所示,则该几何体的体积为
(2013•丽水一模)某几何体的三视图如图所示,则该几何体的体积为 (2013•丽水一模)已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1),
(2013•丽水一模)已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1),