题目内容
类比“二倍角的正、余弦公式”的形式,对于给定的两个函数,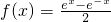 ,
,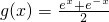 ,给出以下两个式子
,给出以下两个式子
①f(2x)=2f(x)•g(x); ②g(2x)=[g(x)]2-[f(x)]2;
其中正确的是________.
①
分析:写出“二倍角的正弦公式”的形式,据此二倍角公式写出类比结论,最后再进行证明即可.
解答:∵“二倍角的正弦公式”的形式是:
sin2x=2sinxcosx,cos2x=cos2x-sin2x,
有类比结论:
设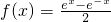 ,
,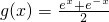 ,有①f(2x)=2f(x)•g(x); ②g(2x)=[g(x)]2-[f(x)]2;
,有①f(2x)=2f(x)•g(x); ②g(2x)=[g(x)]2-[f(x)]2;
其中①是正确的,证明如下:
∵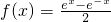 ,
,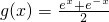 ,
,
∴f(x)g(x)=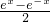 ×
×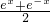 =
= ×
×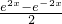 =
= f(2x)
f(2x)
∴f(2x)=2f(x)g(x).
②是不正确的,∵证明如下:
由于g(2x)= ,
,
[g(x)]2-[f(x)]2= -
- =1,
=1,
故②不正确.
故答案为:①.
点评:本题考查利用类比推理从形式上写出类比结论,写类比结论时:先找类比对象,再找类比元素.
分析:写出“二倍角的正弦公式”的形式,据此二倍角公式写出类比结论,最后再进行证明即可.
解答:∵“二倍角的正弦公式”的形式是:
sin2x=2sinxcosx,cos2x=cos2x-sin2x,
有类比结论:
设
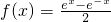 ,
,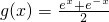 ,有①f(2x)=2f(x)•g(x); ②g(2x)=[g(x)]2-[f(x)]2;
,有①f(2x)=2f(x)•g(x); ②g(2x)=[g(x)]2-[f(x)]2;其中①是正确的,证明如下:
∵
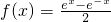 ,
,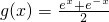 ,
,∴f(x)g(x)=
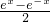 ×
×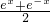 =
= ×
×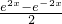 =
= f(2x)
f(2x)∴f(2x)=2f(x)g(x).
②是不正确的,∵证明如下:
由于g(2x)=
 ,
,[g(x)]2-[f(x)]2=
 -
- =1,
=1,故②不正确.
故答案为:①.
点评:本题考查利用类比推理从形式上写出类比结论,写类比结论时:先找类比对象,再找类比元素.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 ,ak=
,ak= ,则该数列前mk项之和是________.
,则该数列前mk项之和是________.



 >0的解集是(-∞,-5)∪(-2,-1),那么m的值是________.
>0的解集是(-∞,-5)∪(-2,-1),那么m的值是________. <x<1+
<x<1+ ,若z=x2+y2的最小值为
,若z=x2+y2的最小值为 有最小值为________.
有最小值为________.