题目内容
设数列{an}的前n项和为Sn,满足2Sn=an+1-2n+1+1,n∈N*,且a1,a2+5,a3成等差数列.
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有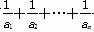 <
<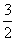 .
.
解:(1 )∵a1,a2+5,a3成等差数列,
)∵a1,a2+5,a3成等差数列,
∴2(a2+5)=a1+a3.
又∵2a1 =2S1=a2-22+1,2(a1+a2)
=2S1=a2-22+1,2(a1+a2) =2S2=a3-23+1,
=2S2=a3-23+1,
∴a2=2a1+3,a3=6a1+13.
因此4a1+16=7a1+13,从而a1=1.
(2)由题设条件知,n≥2时,2Sn-1=an-2n+1,
2Sn=an+1-2n+1+1.
∴2an=an+1-an-2n,于是
an+1=3an+2n(n≥2).
而由(1)知,a2=2a1+3=5=3a1+2,
因此对一切正整数n,有an+1=3an+2n,
所以an+1+2n +1=3(an+2n).
+1=3(an+2n).
又∵a1+21=3,
∴{an+2n}是以3为首项,3为公比的等比数列.
故an+2n=3n,即an=3n-2n.
(3)证明:∵an=3n-2n=3·3n-1-2n=3n-1+2(3n-1-2n-1)≥3n-1,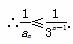
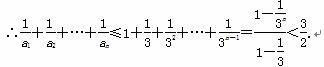

练习册系列答案
相关题目
 )n-1
)n-1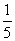 .第一个月的经营收入约为40万元,预计以后每个月收入会比上个月增加
.第一个月的经营收入约为40万元,预计以后每个月收入会比上个月增加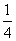 .
. B.充分不必要条件
B.充分不必要条件 C.充分必要条件 D.既不充分也不必要条件
C.充分必要条件 D.既不充分也不必要条件 或b>
或b> ”的( )
”的( ) D.既不充分也不必要条件
D.既不充分也不必要条件 +3y的最小值为________.
+3y的最小值为________. 76
76