题目内容
12.已知函数f(x)=sin(2x+$\frac{π}{6}$)+2sin2x(1)求函数f(x)的最小正周期;
(2)求函数f(x)的最大值和最小值.
分析 化简f(x)为正弦型函数,由此求出(1)函数f(x)的最小正周期T;(2)函数f(x)的最大值与最小值.
解答 解:函数f(x)=sin(2x+$\frac{π}{6}$)+2sin2x
=sin2xcos$\frac{π}{6}$+cos2xsin$\frac{π}{6}$+2•$\frac{1-cos2x}{2}$
=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x+1
=sin(2x-$\frac{π}{6}$)+1,
(1)函数f(x)的最小正周期为T=$\frac{2π}{2}$=π;
(2)令2x-$\frac{π}{6}$=$\frac{π}{2}$+2kπ,k∈Z,得x=$\frac{π}{3}$+kπ,k∈Z,
此时sin(2x-$\frac{π}{6}$)取得最大值1,对应函数f(x)取得最大值为1+1=2;
令2x-$\frac{π}{6}$=-$\frac{π}{2}$+2kπ,k∈Z,得x=-$\frac{π}{6}$+kπ,k∈Z,
此时sin(2x-$\frac{π}{6}$)取得最小值-1,对应函数f(x)取得最小值为1-1=0.
点评 本题考查了三角函数的图象与性质的应用问题,也考查了三角恒等变换的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.设数列{an}是等差数列,且a4=-4,a9=4,Sn是数列{an}的前n项和,则( )
| A. | S5<S6 | B. | S5=S6 | C. | S7=S5 | D. | S7=S6. |
17.已知下列随机变量:
①10件产品中有2件次品,从中任选3件,取到次品的件数X;
②一位射击手对目标进行射击,击中目标得1分,未击中目标得0分,用X表示该射击手在一次射击中的得分;
③刘翔在一次110米跨栏比赛中的成绩X;
④在体育彩票的抽奖中,一次摇号产生的号码数X.
其中X是离散型随机变量的是( )
①10件产品中有2件次品,从中任选3件,取到次品的件数X;
②一位射击手对目标进行射击,击中目标得1分,未击中目标得0分,用X表示该射击手在一次射击中的得分;
③刘翔在一次110米跨栏比赛中的成绩X;
④在体育彩票的抽奖中,一次摇号产生的号码数X.
其中X是离散型随机变量的是( )
| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ③④ |
4.如图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第n个图案中需用黑色瓷砖块数为( )
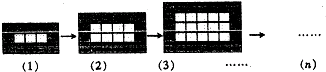

| A. | 4n+2 | B. | 4n+4 | C. | 4n+6 | D. | 4n+8 |
2.设数列{an}是公差不为零的等差数列,且a1,a3,a7构成等比数列,则公比q为( )
| A. | $\sqrt{2}$ | B. | 4 | C. | 2 | D. | $\frac{1}{2}$ |
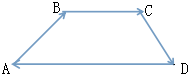 如图所示的四边形ABCD,已知$\overrightarrow{AB}$=(6,1),$\overrightarrow{BC}$=(x,y),$\overrightarrow{CD}$=(-2,-3)
如图所示的四边形ABCD,已知$\overrightarrow{AB}$=(6,1),$\overrightarrow{BC}$=(x,y),$\overrightarrow{CD}$=(-2,-3)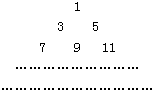 把正奇数数列{2n-1}中的数按上小下大、左小右大的原则排成如图三角形数表:
把正奇数数列{2n-1}中的数按上小下大、左小右大的原则排成如图三角形数表: