题目内容
如图所示,已知椭圆的方程为  ,A为椭圆的左顶点,B,C在椭圆上,若四边形OABC为平行四边形,且∠OAB=45°,则椭圆的离心率等于( )
,A为椭圆的左顶点,B,C在椭圆上,若四边形OABC为平行四边形,且∠OAB=45°,则椭圆的离心率等于( )
A. | B. | C. | D. |
C
解析试题分析:由图形知|BC|=a,且BC∥OA由椭圆的对称性知,B,C两点关于y轴对称,由此可以求出两点的坐标,再连接OC,有∠OAB=45°及平行的性质,椭圆的对称性,令椭圆的右端点为M,则有∠COM=∠CMO=∠OAB=45°由此可得CO垂直于MC,故有
又四边形OABC为平行四边形,B,C在椭圆上,由图形知|BC|=a,且BC∥OA由椭圆的对称性知,B,C两点关于y轴对称,故C的横坐标为 ,代入椭圆方程
,代入椭圆方程 中,则有
中,则有 ,那么代入上式可知a2=3b2,故可得c2=2b2,所以椭圆的离心率等于
,那么代入上式可知a2=3b2,故可得c2=2b2,所以椭圆的离心率等于 ,选C
,选C
考点:椭圆的简单性质
点评:本题考查椭圆的简单性质,求解本题的关键是根据椭圆的对称性得出点C的坐标以及图形中的垂直关系,求出点C的坐标是为了表示出斜率,求出垂直关系是为了利用斜率的乘积为-1建立方程,然后再根据求离心率的公式求出离心率即可.本题比较抽象,方法单一,入手较难,运算量不大

练习册系列答案
相关题目
若以椭圆上一点和两个焦点为顶点的三角形面积的最大值为1,则椭圆长轴的最小值为( )
| A.1 | B. | C.2 | D.2 |
双曲线 的实轴长是( )
的实轴长是( )
| A.2 | B.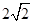 | C.4 | D.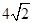 |
在区间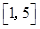 和
和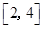 分别取一个数,记为
分别取一个数,记为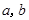 ,则方程
,则方程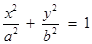 表示焦点在
表示焦点在 轴上且离心率小于
轴上且离心率小于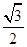 的椭圆的概率为
的椭圆的概率为
A.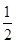 | B.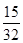 | C.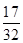 | D.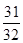 |
若点 到双曲线
到双曲线
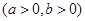 的一条渐近线的距离为
的一条渐近线的距离为 ,则该双曲线的离心率为
,则该双曲线的离心率为
A. | B. | C. | D. |
已知焦点在x轴上的双曲线的渐近线方程是y=±4x,则该双曲线的离心率是( )
A. | B. | C. | D. |
已知 是椭圆
是椭圆 的两个焦点,经过点
的两个焦点,经过点 的直线交椭圆于点
的直线交椭圆于点 ,若
,若 ,则
,则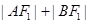 等于( )
等于( )
A. | B. | C. | D. |
 上,那么点P到点Q(2,1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
上,那么点P到点Q(2,1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
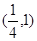


 在抛物线
在抛物线 上,那么
上,那么 的距离与点
的距离与点


