题目内容
在区间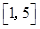 和
和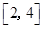 分别取一个数,记为
分别取一个数,记为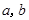 ,则方程
,则方程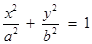 表示焦点在
表示焦点在 轴上且离心率小于
轴上且离心率小于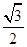 的椭圆的概率为
的椭圆的概率为
A.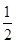 | B.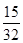 | C.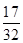 | D.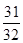 |
B
解析试题分析:∵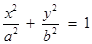 表示焦点在x轴上且离心率小于
表示焦点在x轴上且离心率小于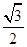 ,∴a>b>0,a<2b,
,∴a>b>0,a<2b,
它对应的平面区域如图中阴影部分所示: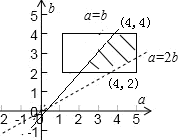
则方程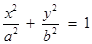 表示焦点在x轴上且离心率小于
表示焦点在x轴上且离心率小于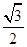 的椭圆的概率为
的椭圆的概率为
P=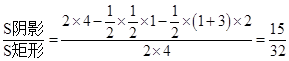 ,故选B.
,故选B.
考点:本题主要考查椭圆的几何性质,平面区域的面积计算,几何概型概率的计算。
点评:小综合题,几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关。

练习册系列答案
相关题目
设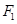 和
和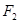 为双曲线
为双曲线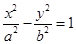 (
(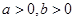 )的两个焦点, 若点
)的两个焦点, 若点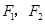 和点
和点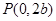 是正三角形的三个顶点,则双曲线的离心率为( )。
是正三角形的三个顶点,则双曲线的离心率为( )。
A.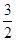 | B.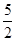 | C.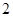 | D.3 |
抛物线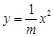 的焦点坐标为( )
的焦点坐标为( )
A.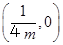 | B.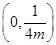 | C.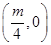 | D.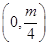 |
抛物线y=x2在点M(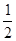 ,
,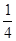 )处的切线的倾斜角是( )
)处的切线的倾斜角是( )
| A.30° | B.45° | C.60° | D.90° |
若双曲线 的离心率为2,则双曲线
的离心率为2,则双曲线 的离心率为( )
的离心率为( )
A. | B. | C.2 | D. |
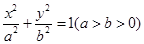 与双曲线
与双曲线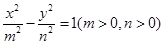 有相同的焦点
有相同的焦点 和
和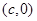 ,若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率为
,若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率为

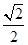
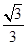
 ,A为椭圆的左顶点,B,C在椭圆上,若四边形OABC为平行四边形,且∠OAB=45°,则椭圆的离心率等于( )
,A为椭圆的左顶点,B,C在椭圆上,若四边形OABC为平行四边形,且∠OAB=45°,则椭圆的离心率等于( )




 和
和 为双曲线
为双曲线 (
( )的两个焦点, 若点
)的两个焦点, 若点 和点
和点 是正三角形的三个顶点,则双曲线的离心率为( )。
是正三角形的三个顶点,则双曲线的离心率为( )。


 的左右焦点分别为
的左右焦点分别为 ,若椭圆
,若椭圆 上恰好有6个不同的点
上恰好有6个不同的点 ,使得
,使得 为等腰三角形,则椭圆
为等腰三角形,则椭圆


