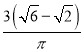题目内容
【题目】已知函数![]() 的最大值为
的最大值为![]() ,且曲线
,且曲线![]() 在x=0处的切线与直线
在x=0处的切线与直线![]() 平行(其中e为自然对数的底数).
平行(其中e为自然对数的底数).
(1)求实数a,b的值;
(2)如果![]() ,且
,且![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)对原函数求导数,然后利用在x=0处切线的斜率为1,函数的最大值为![]() 列出关于a,b的方程组求解;
列出关于a,b的方程组求解;
(2)利用![]() 找到
找到![]() 的关系式
的关系式![]() ,然后引入
,然后引入![]() ,构造关于t的函数,将
,构造关于t的函数,将![]() 转换成关于t的函数,求最值即可.
转换成关于t的函数,求最值即可.
解:(1)由已知![]() .
.
则易知![]() ,又因为
,又因为![]() ,故a=0.
,故a=0.
此时可得![]() .
.
①若b>0,则当![]() 时,
时,![]() 递减;
递减;
当![]() 时,
时,![]() 递增.
递增.
此时,函数![]() 有最小值,无最大值.
有最小值,无最大值.
②若b<0,则当![]() 时,
时,![]() 递增;
递增;
当![]() 时,
时,![]() 递减.
递减.
此时![]() ,解得
,解得![]() .
.
所以![]() 即为所求.
即为所求.
(2)由![]() ,且
,且![]() 得:
得:![]() .
.
∴![]() .设
.设![]() ,则
,则![]()
可得![]() ,所以要证
,所以要证![]() ,即证
,即证![]() .
.
∵t>0,所以![]() ,所以即证
,所以即证![]() .
.
设![]() ,则
,则![]() .
.
令![]() ,则
,则![]()
当![]() 时,
时,![]() 递减;当
递减;当![]() 时,
时,![]() 递增.
递增.
所以![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 上递增.
上递增.
所以![]() .
.
![]() .
.

练习册系列答案
相关题目