Question

【题目】如图,已知抛物线E:y2=4x与圆M:(x3)2+y2=r2(r>0)相交于A,B,C,D四个点.

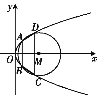
(1)求r的取值范围;

(2)设四边形ABCD的面积为S,当S最大时,求直线AD与直线BC的交点P的坐标.

Answer 1

【答案】(1) r∈(2,3). (2) (,0).

【解析】

(1)联立抛物线与圆的方程，利用判别式与韦达定理列不等式组，从而可得结果；(2)根据S=(+)·(x2x1)=(4+4)(x2x1)，利用韦达定理将S表示为关于r的函数，换元后利用导数可求当S最大时直线AD与直线BC的交点P的坐标.

(1)联立抛物线与圆的方程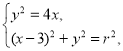

消去y,得x22x+9r2=0.

由题意可知x22x+9r2=0在(0,+∞)上有两个不等的实数根,

所以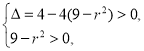解得2<r<3,即r∈(2,3).

(2)根据(1)可设方程x22x+9r2=0的两个根分别为x1,x2(0<x1<x2),

则A(x1,2),B(x1, 2),C(x2, 2),D(x2,2),且x1+x2=2,x1x2=9r2,

所以S=(+)·(x2x1)=(4+4)(x2x1)

=2·=2·.

令t=∈(0,1),f(t)=S2=4(2+2t)(44t2)= 32(t3+t2t1),

f'(t)= 32(3t2+2t1)= 32(t+1)(3t1),可得f(t)在(0,)上单调递增,在(,1)上单调递减,即当t=时,四边形ABCD的面积取得最大值.

根据抛物线与圆的对称性,可设P点坐标为(m,0),由P,A,D三点共线,可得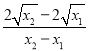=,整理得m==t=,

所以点P的坐标为(,0).