题目内容
【题目】设抛物线![]() 的方程为
的方程为![]() ,其中常数
,其中常数![]() ,F是抛物线
,F是抛物线![]() 的焦点.
的焦点.
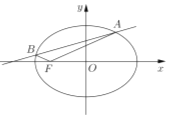
(1)设A是点F关于顶点O的对称点,P是抛物线![]() 上的动点,求
上的动点,求![]() 的最大值;
的最大值;
(2)设![]() ,
,![]() ,
,![]() 是两条互相垂直,且均经过点F的直线,
是两条互相垂直,且均经过点F的直线,![]() 与抛物线
与抛物线![]() 交于点A,B,
交于点A,B,![]() 与抛物线
与抛物线![]() 交于点C,D,若点G满足
交于点C,D,若点G满足![]() ,求点G的轨迹方程.
,求点G的轨迹方程.
【答案】(1)最大值为![]() ;(2)
;(2)![]()
【解析】
(1)求得A的坐标,设出过A的直线为y=k(x![]() ),k=tanα,联立抛物线方程,运用判别式为0,求得倾斜角,可得所求最大值;
),k=tanα,联立抛物线方程,运用判别式为0,求得倾斜角,可得所求最大值;
(2)求得F(1,0),设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),G(x,y),设l1:y=k(x﹣1),联立抛物线方程,运用韦达定理,以及两直线垂直的条件:斜率之积为﹣1,结合向量的坐标表示,以及消元,可得所求轨迹方程.
(1)A是点![]() 关于顶点O的对称点,可得
关于顶点O的对称点,可得![]() ,
,
设过A的直线为![]() ,
,![]() ,
,
联立抛物线方程可得![]() ,
,
由直线和抛物线相切可得![]() ,解得
,解得![]() ,
,
可取![]() ,可得切线的倾斜角为45°,
,可得切线的倾斜角为45°,
由抛物线的定义可得![]() ,而
,而![]() 的最小值为45°,
的最小值为45°,
![]() 的最大值为
的最大值为![]() ;
;
(2)由![]() ,可得
,可得![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() ,联立抛物线
,联立抛物线![]() ,可得
,可得![]() ,
,
即有![]() ,
,![]() ,
,
由两直线垂直的条件,可将k换为![]() ,可得
,可得![]() ,
,![]() ,
,
点G满足![]() ,可得
,可得![]() ,
,
即为![]() ,
,![]() ,
,
可得![]() ,则G的轨迹方程为
,则G的轨迹方程为![]() .
.

练习册系列答案
相关题目