题目内容
设a∈R，函数f （x）=ex+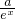
是偶函数，若曲线y=f （x）的一条切线的斜率是
，则切点的横坐标为________．
ln2
分析：先由f（x）为偶函数求出a值，然后求出导数f′（x），令f′（x）=，解出x即为所求．
解答：因为f（x）=ex+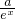是偶函数，所以总有f（-x）=f（x），即
=ex+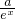，整理得（a-1）（
）=0，所以有a-1=0，即a=1．
则f（x）=
，f′（x）=ex-
，令f′（x）=ex-=，整理即为2e2x-3ex-2=0，解得ex=2，所以x=ln2．
故答案为：ln2．
点评：本题考查函数的奇偶性及导数的几何意义，若f（x）为偶函数，则f（-x）=f（x）恒成立．
分析：先由f（x）为偶函数求出a值，然后求出导数f′（x），令f′（x）=
，解出x即为所求．解答：因为f（x）=ex+
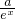是偶函数，所以总有f（-x）=f（x），即=ex+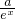，整理得（a-1）（）=0，所以有a-1=0，即a=1．则f（x）=
，f′（x）=ex-，令f′（x）=ex-=，整理即为2e2x-3ex-2=0，解得ex=2，所以x=ln2．故答案为：ln2．
点评：本题考查函数的奇偶性及导数的几何意义，若f（x）为偶函数，则f（-x）=f（x）恒成立．
练习册系列答案
相关题目