题目内容
一个袋子中装有6个红球和4个白球,假设袋子中的每一个球被摸到可能性是相等的.(Ⅰ)从袋子中任意摸出3个球,求摸出的球均为白球的概率;
(Ⅱ)一次从袋子中任意摸出3个球,若其中红球的个数多于白球的个数,则称“摸球成功”(每次操作完成后将球放回).M某人连续摸了3次,记“摸球成功”的次数为ξ,求ξ的分布列和数学期望.
【答案】分析:(Ⅰ)设从袋子中任意摸出3个球,利用排列组合知识能求出摸出的球均为白球的概率.
(Ⅱ)由一次”摸球成功”的概率P= =
= .随机变量ξ服从二项分布B(3,
.随机变量ξ服从二项分布B(3, ),由此能求出ξ的分布列和数学期望.
),由此能求出ξ的分布列和数学期望.
解答:解:(Ⅰ)设从袋子中任意摸出3个球,摸出的球均为白球的概率:
P= =
= .…(4分)
.…(4分)
(Ⅱ)由一次”摸球成功”的概率P= =
= .…(8分)
.…(8分)
随机变量ξ服从二项分布B(3, ),
),
∴ξ的分布列为:…(12分)
Eξ=3× =2. …(14分)
=2. …(14分)
点评:本题考查离散型随机变量的分布列和数学期望,在历年高考中都是必考题型.解题时要认真审题,注意概率知识的灵活运用.
(Ⅱ)由一次”摸球成功”的概率P=
 =
= .随机变量ξ服从二项分布B(3,
.随机变量ξ服从二项分布B(3, ),由此能求出ξ的分布列和数学期望.
),由此能求出ξ的分布列和数学期望.解答:解:(Ⅰ)设从袋子中任意摸出3个球,摸出的球均为白球的概率:
P=
 =
= .…(4分)
.…(4分)(Ⅱ)由一次”摸球成功”的概率P=
 =
= .…(8分)
.…(8分)随机变量ξ服从二项分布B(3,
 ),
),∴ξ的分布列为:…(12分)
| ξ | 1 | 2 | 3 | |
| P |  |  |  |  |
 =2. …(14分)
=2. …(14分)点评:本题考查离散型随机变量的分布列和数学期望,在历年高考中都是必考题型.解题时要认真审题,注意概率知识的灵活运用.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
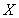
 ,求
,求