题目内容
一个袋子中装有6个红球和4个白球,假设每一个球被摸到的可能性是相等的.
(I)从袋子中摸出3个球,求摸出的球为2个红球和1个白球的概率;
(II)从袋子中摸出2个球,其中白球的个数为ξ,求ξ的分布列和数学期望.
(I)从袋子中摸出3个球,求摸出的球为2个红球和1个白球的概率;
(II)从袋子中摸出2个球,其中白球的个数为ξ,求ξ的分布列和数学期望.
分析:(I)从10个球中任取3个球有
种方法,从6个白球中任取2个有
中方法,从4个白球中任取一个有
中方法,利用乘法原理可得:摸出的球为2个红球和1个白球的方法为
,再利用古典概型的概率计算公式即可得出.
(II)ξ=0,1,2.利用“超几何分布”的概率计算公式P(ξ=k)=
(k=0,1,2)可得其分布列.再利用数学期望计算公式即可得出.
| C | 3 10 |
| C | 2 6 |
| C | 1 4 |
| C | 2 6 |
| C | 1 4 |
(II)ξ=0,1,2.利用“超几何分布”的概率计算公式P(ξ=k)=
| ||||
|
解答:解:(I)从10个球中任取3个球有
种方法,从6个白球中任取2个有
中方法,从4个白球中任取一个有
中方法,可得摸出的球为2个红球和1个白球的方法为
,
∴P=
=
;
(II)ξ=0,1,2.由“超几何分布”可得:P(ξ=k)=
(k=0,1,2).
∴Eξ=0+1×
+2×
=
| C | 3 10 |
| C | 2 6 |
| C | 1 4 |
| C | 2 6 |
| C | 1 4 |
∴P=
| ||||
|
| 1 |
| 2 |
(II)ξ=0,1,2.由“超几何分布”可得:P(ξ=k)=
| ||||
|
| ξ | 0 | 1 | 2 | ||||||
| p(ξ) |
|
|
|
| 8 |
| 15 |
| 2 |
| 15 |
| 4 |
| 5 |
点评:本题考查了古典概型的概率计算公式、超几何分布列及其数学期望、乘法原理、组合数的计算公式等基础知识与基本技能方法,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
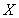
 ,求
,求