题目内容
9.“x+3=0”是“x2-9=0”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既充分也不必要条件 |
分析 由x2-9=0,解得x=±3.即可判断出结论.
解答 解:由x2-9=0,解得x=±3.
∴“x+3=0”是“x2-9=0”充分不必要条件,
故选:A.
点评 本题考查了方程的解法、充要条件的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
19.已知向量$\overline{a}$=(1,-$\sqrt{3}$),$\overline{b}$=(-2,0),则$\overline{a}$与$\overline{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
17.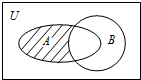 已知全集U=R,集合$A=\{\;x|\;{(\frac{1}{2})^x}≤1\;\}$,B={x|x2-6x+8≤0},则图中阴影部分所表示的集合为( )
已知全集U=R,集合$A=\{\;x|\;{(\frac{1}{2})^x}≤1\;\}$,B={x|x2-6x+8≤0},则图中阴影部分所表示的集合为( )
 已知全集U=R,集合$A=\{\;x|\;{(\frac{1}{2})^x}≤1\;\}$,B={x|x2-6x+8≤0},则图中阴影部分所表示的集合为( )
已知全集U=R,集合$A=\{\;x|\;{(\frac{1}{2})^x}≤1\;\}$,B={x|x2-6x+8≤0},则图中阴影部分所表示的集合为( )| A. | {x|x≤0} | B. | {x|2≤x≤4} | C. | {x|0<x≤2或x≥4} | D. | {x|0≤x<2或x>4} |
1.若y=f(x2),则y′等于( )
| A. | 2xf′(x2) | B. | 2xf′(x) | C. | 4x2f(x) | D. | f′(x2) |
19.终边在坐标轴上的角的集合是( )
| A. | {α|α=2kπ,k∈Z} | B. | {α|α=kπ,k∈Z} | C. | {α|α=kπ+$\frac{π}{2}$,K∈Z} | D. | {α|α=$\frac{1}{2}kπ$,k∈Z} |
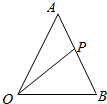 如图,在△OAB中,点P为线段AB上的一个动点(不包含端点),且满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$.
如图,在△OAB中,点P为线段AB上的一个动点(不包含端点),且满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$.