题目内容
5.设数列{an}的前n项和为Sn,a4=7且4Sn=n(an+an+1),则S10等于( )| A. | 90 | B. | 100 | C. | 110 | D. | 120 |
分析 由题意可得4S3=3(a3+7),4S2=2(a2+a3),4S1=a1+a2,运用数列的递推式可得a1=1,a2=3,a3=5,进而得到an=2n-1,${S_n}={n^2}$,即可得到所求值.
解答 解:由数列{an}的前n项和为Sn,a4=7且4Sn=n(an+an+1),
可得4S3=3(a3+7),4S2=2(a2+a3),4S1=a1+a2,
∴a2=3a1,a3=5a1,
从而4×9a1=3(5a1+7),
即a1=1,∴a2=3,a3=5,
∴4S4=4(a4+a5),
∴a5=9,同理得a7=13,a8=15,…,an=2n-1,
∴${S_n}={n^2}$,经验证4Sn=n(an+an+1)成立,
∴S10=100.
故选:B.
点评 本题考查数列的通项公式和前n项和的求法,注意运用数列递推式,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
13.已知命题p:“?x∈R,使得x-2>lgx”,命题q:“?a∈R*,$\frac{x^2}{4}+\frac{y^2}{a}=1$表示椭圆”,则下列命题为真的是( )
| A. | p∧q | B. | (¬p)∨q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |
17.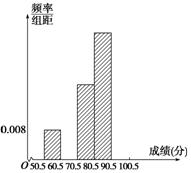 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),解答下列问题:
(1)填充频率分布表中的空格;
(2)补全频率分布直方图;
(3)若成绩在80.5~90.5分的学生可以获得二等奖,问获得二等奖的学生约为多少人?
 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),解答下列问题:| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 0.16 | |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | ||
| 合计 | 50 |
(2)补全频率分布直方图;
(3)若成绩在80.5~90.5分的学生可以获得二等奖,问获得二等奖的学生约为多少人?
14.一辆卡车宽2.7米,要经过一个半径为4.5米的半圆形隧道(双车道,不得违章),则这辆卡车的平顶车篷篷顶距离地面的高度不得超过( )米.
| A. | 1.4 | B. | 3.0 | C. | 3.6 | D. | 4.5 |
15.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),A,B为双曲线的左右顶点,若点M在双曲线上,且满足△ABM为一个顶角为120°的等腰三角形,则双曲线的渐近线方程是( )
| A. | y=±x | B. | y=±$\sqrt{2}$x | C. | y=±2x | D. | y=±$\frac{\sqrt{2}}{2}$x |