题目内容
在锐角△ABC中，角A、B、C所对的边长分别为a、b、c.向量m＝(1，cosB)，n＝(sinB，－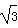
)，且m⊥n.
(1) 求角B的大小；
(2) 若△ABC面积为10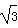，b＝7，求此三角形周长．
解：(1) m·n＝sinB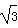－cosB，∵ m⊥n，∴ m·n＝0，
∴ sinB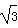－cosB＝0.∵ △ABC为锐角三角形，∴ cosB≠0，
∴ tanB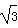＝.∵ 0<B<
，∴ B＝
.
(2) ∵ S△ABC＝
acsinB＝
ac，由题设ac＝10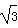，得ac＝40.由72＝a2＋c2－2accosB，得49＝a2＋c2－ac，∴ (a＋c)2＝(a2＋c2－ac)＋3ac＝49＋120＝169.∴ a＋c＝13，
∴ 三角形周长是20.
练习册系列答案
相关题目
的最大值和最小值；
，则sin(x＋y)＝________．
，sinβ＝
，且α、β均为锐角，求α＋β的值．
，则cos2α＝________．
，则cos2α＋cos2β＋
cosαcosβ＝________．
，且α∈
，则sin4α－cos4α＝________．
，sinβ＝
，且α、β为锐角，则α＋β的值为__________．