Question

如图2，直三棱柱中，，，棱，、分别是、的中点．

⑴ 求证：平面；

⑵ 求直线与平面所成角的正弦值．

Answer 1

证明与求解：⑴，底面，

，， ，因为，，，所以平面 ， ，因为，所以平面

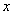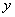⑵（方法一）以C为原点，CA、CB、CC₁在直线分别为轴、轴、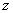轴建立空间直角坐标系 ，

则、、 ，

、 ，

、、 ，

设平面的一个法向为，则 ，

即，取 ，

所以 ， 。

（方法二），， 分，所以，，… ，由⑴知，，所以平面……8分。

延长到，延长到，使，连接、 ，在中，，， ，

 ，

是平面的法向量，由所作知，从而，所以 。

其他方法，例如将直三棱柱补成长方体，可参照给分。