题目内容
已知g（x）=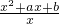
，x∈（0，+∞），是否存在实数a，b，使g（x）同时满足下列两个条件：（1）g（x）在（0，1）上是减函数，在[1，+∞）上是增函数；（2）g（x）的最小值是3．若存在，求出a、b，若不存在，说明理由．
解：∵g（x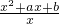）=，∴g′（x）=1-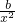
∵g（x）在（0，1）上是减函数，在[1，+∞）上是增函数，
∴g′（1）=0，∴b=1
∵g（x）的最小值是3
∴g（1）=1+a+b=3，∴a=1
综上，a=1，b=1．
分析：求导函数，利用函数的单调性，可得g′（1）=0，利用g（x）的最小值是3，可得g（1）=0，由此即可得到结论．
点评：本题考查函数的单调性与最值，考查学生分析解决问题的能力，正确运用函数的单调性与最值是关键．
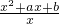，∴g′（x）=1-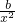∵g（x）在（0，1）上是减函数，在[1，+∞）上是增函数，
∴g′（1）=0，∴b=1
∵g（x）的最小值是3
∴g（1）=1+a+b=3，∴a=1
综上，a=1，b=1．
分析：求导函数，利用函数的单调性，可得g′（1）=0，利用g（x）的最小值是3，可得g（1）=0，由此即可得到结论．
点评：本题考查函数的单调性与最值，考查学生分析解决问题的能力，正确运用函数的单调性与最值是关键．
练习册系列答案
相关题目
，设g（x）是函数f（x）在区间[0，+∞）上的导函数，问是否存在实数a，满足a＞1并且使g（x）在区间
上的值域为
，若存在，求出a的值；若不存在，请说明理由．
sin（2x+
），f（x）=acos2（x+
）+b，且函数y=f（x）的图象是函数y=g（x）的图象按向量a=（-
，
f（x），求h（x）的最小值及相应的x的值．
sin（2x+
），f（x）=acos2（x+
）+b，且函数y=f（x）的图象是函数y=g（x）的图象按向量a=（-
，
）平移得到的．
f（x），求h（x）的最小值及相应的x的值．