题目内容
12. 如图,在△ABC中,|$\overrightarrow{AB}$|=3,|$\overrightarrow{AC}$|=1,BC中点为D,E为线段AD上的任意一点.
如图,在△ABC中,|$\overrightarrow{AB}$|=3,|$\overrightarrow{AC}$|=1,BC中点为D,E为线段AD上的任意一点.(1)求$\overrightarrow{AD}$•($\overrightarrow{AB}$-$\overrightarrow{AC}$)的值;
(2)若AC⊥BC,求$\overrightarrow{AE}$•($\overrightarrow{EB}$+$\overrightarrow{EC}$)的最大值.
分析 (1)运用向量的中点表示和向量的平方即为模的平方,计算即可得到所求值;
(2)运用勾股定理,可得AD=$\sqrt{3}$,再由中点的斜率表示和向量的数量积的定义,结合基本不等式,即可得到所求的最大值.
解答 解:(1)由AD为△ABC的中线,可得
$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
则$\overrightarrow{AD}$•($\overrightarrow{AB}$-$\overrightarrow{AC}$)=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)•($\overrightarrow{AB}$-$\overrightarrow{AC}$)=$\frac{1}{2}$($\overrightarrow{AB}$2-$\overrightarrow{AC}$2)
=$\frac{1}{2}$×(32-12)=4;
(2)AC⊥BC,即有BC2=AB2-AC2=9-1=8,
可得BC=2$\sqrt{2}$,CD=$\sqrt{2}$,
AD2=AC2+CD2=1+2=3,即AD=$\sqrt{3}$,
则$\overrightarrow{AE}$•($\overrightarrow{EB}$+$\overrightarrow{EC}$)=$\overrightarrow{AE}$•2$\overrightarrow{ED}$
=2|$\overrightarrow{AE}$|•|$\overrightarrow{ED}$|•cos0=2|$\overrightarrow{AE}$|•|$\overrightarrow{ED}$|,
设|$\overrightarrow{AE}$|=t(0≤t≤$\sqrt{3}$),则|$\overrightarrow{ED}$|=$\sqrt{3}$-t,
即有$\overrightarrow{AE}$•($\overrightarrow{EB}$+$\overrightarrow{EC}$)=2t($\sqrt{3}$-t)≤2•($\frac{t+\sqrt{3}-t}{2}$)2=$\frac{3}{2}$,
当且仅当t=$\frac{\sqrt{3}}{2}$,即E为AD的中点时,取得最大值$\frac{3}{2}$.
点评 本题考查向量的数量积的定义和性质,考查最值的求法,注意运用换元法结合基本不等式,考查运算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
| A. | -120 | B. | 120 | C. | -45 | D. | 45 |
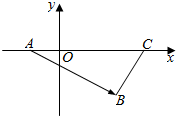 如图,在△ABC中,点A,C在x轴上,AB=4,∠BAC=30°,求向量$\overrightarrow{AB}$的坐标.
如图,在△ABC中,点A,C在x轴上,AB=4,∠BAC=30°,求向量$\overrightarrow{AB}$的坐标.