题目内容
已知集合A={x|x∈N，x≤4}，B={x|x∈N，x＞1}，则A∩B等于（ ）
| A、{1，2，3，4} |
| B、{2，3} |
| C、{2，3，4} |
| D、{x|1＜x≤4，x∈R} |
考点：交集及其运算
专题：集合
分析：直接利用查两个集合的交集的定义求得A∩B．
解答：
解：∵A={x|x∈N，x≤4}={0，1，2，3，4 }，B={x|x∈N，x＞1}，
∴A∩B={2，3，4}，
故选：C．
∴A∩B={2，3，4}，
故选：C．
点评：本题主要考查两个集合的交集的定义和求法，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在复平面内，复数z=
对应的点位于（ ）
| 1-i |
| 2+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知集合M={x|
＞0}，N={x|3x+2＞0}，则M∩N=（ ）
| x-3 |
| x+1 |
| A、（-∞，-1） | ||
B、（-1，-
| ||
C、（-
| ||
| D、（3，+∞） |
在下面哪个区间内函数y=x2-4x+3与函数y=lnx-2x都为减函数（ ）
| A、（-∞，2） | ||
| B、（0，e） | ||
C、(
| ||
| D、（e，+∞） |
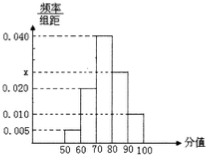为了全面推进素质教育，教育部门对某省500所中小学进行调研考评，考评分数在80分以上（含80分）的授予“素质教育先进学校”称号，考评统计结果如图的频率分布直方图所示，则应授予“素质教育先进学校”称号的学校有（ ）所．| A、125 | B、175 |
| C、325 | D、50 |
已知圆O：x2+y2=r2，点P（a，b）（ab≠0）是圆O内的一点，过点P的圆O的最短弦在直线l1上，直线l2的方程为bx-ay=r2，那么（ ）
| A、l1∥l2且l2与圆O相交 |
| B、l1⊥l2且l2与圆O相切 |
| C、l1∥l2且l2与圆O相离 |
| D、l1⊥l2且l2与圆O相离 |
已知命题p：?x∈R，x+
≥2，命题q：?x∈R，sinx+cosx=
，下列结论正确的是（ ）
| 1 |
| x |
| 2 |
| A、命题“p∧q”是真命题 |
| B、命题“（￢p）∧q”是真命题 |
| C、命题“（￢p）∨q”是假命题 |
| D、命题“（￢p）∨（￢q）”是假命题 |