题目内容

15．一个容量为100的样本，其数据的分组与各组的参数如下：（0，10〕，12；（10，20〕，13；（20，30〕，15；（30，40〕，24；（40，50〕，16；（50，60〕，13；（60，70〕，7；则这样本数据落在（10，40〕上的频率为（　　）
A．0.13B．0.39C．0.52D．0.64

分析 根据题意，利用频率=$\frac{频数}{样本容量}$，求出答案即可．

解答 解：数据落在（10，40〕上的个数是13+15+24=52，
所以数据落在（10，40〕上的频率为$\frac{52}{100}$=0.52．
故选：C．

点评 本题考查了频率的计算问题，是基础题目．

练习册系列答案
相关题目
5．已知集合$A=\{x|y=\sqrt{{{log}_2}x}\}，B=\{y|y=\frac{1}{2^x}，x＞0\}$，则A∩CRB=（　　）
A．（0，1）B．（-∞，1]C．[1，+∞）D．φ
6．已知函数f（x-1）的定义域是（1，2），那么f（2x）的定义域是（　　）
A．（0，1）B．（$\frac{1}{2}$，1）C．（-∞，0）D．（0，+∞）
3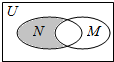．设全集U=R，M={x|x＜-2，或x＞2}，N={x|1＜x＜3}，则图中阴影部分所表示的集合是（　　）
A．{x|-2≤x＜1}B．{x|-2≤x≤2}C．{x|1＜x≤2}D．{x|x＜2}
10．三个数0.42，20.4，log0.42的大小关系为（　　）
A．0.42＜20.4＜log0.42B．log0.42＜0.42＜20.4
C．0.42＜log0.42＜20.4D．log0.42＜20.4＜0.42
20．已知集合M={x|x=$\frac{k}{5}+\frac{1}{10}$，k∈Z} N={x|$\frac{k}{10}+\frac{1}{5}$，k∈Z}，则（　　）
A．M=NB．M⊆NC．M?ND．M∩N=Φ
7．一只装有动力桨的船，其单靠人工划船顺流而下的速度是水速的3倍．现该船靠人工划动从A地顺流到达B地，原路返回时只开足动力桨行驶，用时比来时少$\frac{2}{5}$．问船在静水中开足动力桨行驶的速度是人工划船速度的多少倍？（　　）
A．2B．3C．4D．5
4．若x=-2是关于x的一元二次方程x2-$\frac{5}{2}$ax+a2=0的一个根，则a的值为（　　）
A．1或4B．-1或-4C．-1或4D．1或-4
5．设随机变量X的分布列为P（X=i）=$\frac{i}{2a}$，i=1，2，3，则P（X=2）=$\frac{1}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网