题目内容
5．已知集合$A=\{x|y=\sqrt{{{log}_2}x}\}，B=\{y|y=\frac{1}{2^x}，x＞0\}$，则A∩CRB=（ ）| A． | （0，1） | B． | （-∞，1] | C． | [1，+∞） | D． | φ |
分析 通过对数函数的单调性求出集合A，指数函数的单调性求出集合B，然后求解B的补集，即可求解A∩CRB．
解答 解：因为集合A={x|y=$\sqrt{lo{g}_{2}x}$}={x|x≥1}=[1，+∞），
B={y|y=（$\frac{1}{2}$）x，x＞0}={y|0＜y＜1}=（0，1），
∴CRB=（-∞，0]∪[1，+∞），
∴A∩CRB=[1，+∞），
故选：C．
点评 本题考查集合的交、并、补的基本运算，指数函数与对数函数的单调性的应用，考查计算能力．
练习册系列答案
相关题目
15．
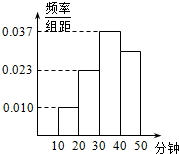某健康协会从某地区睡前看手机的居民中随机选取了n人进行调查，得到如图所示的频率分布直方图．已知睡前看手机时间不低于20分钟的有243人，则n的值为（ ）
某健康协会从某地区睡前看手机的居民中随机选取了n人进行调查，得到如图所示的频率分布直方图．已知睡前看手机时间不低于20分钟的有243人，则n的值为（ ）| A． | 180 | B． | 450 | C． | 360 | D． | 270 |
13．数列{an}中，满足an+2=2an+1-an，且a1，a4031是函数f（x）=$\frac{1}{3}{x^3}-4{x^2}+6x-1$的极值点，则log2a2016的值是（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
10．
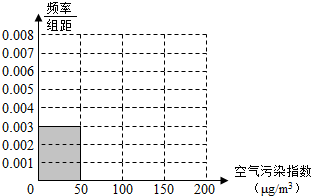空气污染，又称为大气污染，是指由于人类活动或自然过程引起某些物质进入大气中，呈现出足够的浓度，达到足够的时间，并因此危害了人体的舒适、健康和福利或环境的现象．全世界也越来越关注环境保护问题．当空气污染指数（单位：μg/m3）为0～50时，空气质量级别为一级，空气质量状况属于优；当空气污染指数为50～100时，空气质量级别为二级，空气质量状况属于良；当空气污染指数为100～150时，空气质量级别为三级，空气质量状况属于轻度污染；当空气污染指数为150～200时，空气质量级别为四级，空气质量状况属于中度污染；当空气污染指数为200～300时，空气质量级别为五级，空气质量状况属于重度污染；当空气污染指数为300以上时，空气质量级别为六级，空气质量状况属于严重污染．2015年8月某日某省x个监测点数据统计如下：
（Ⅰ）根据所给统计表和频率分布直方图中的信息求出x，y的值，并完成频率分布直方图；
（Ⅱ）在空气污染指数分别为50～100和150～200的监测点中，用分层抽样的方法抽取5个监测点，从中任意选取2个监测点，事件A“两个都为良”发生的概率是多少？
空气污染，又称为大气污染，是指由于人类活动或自然过程引起某些物质进入大气中，呈现出足够的浓度，达到足够的时间，并因此危害了人体的舒适、健康和福利或环境的现象．全世界也越来越关注环境保护问题．当空气污染指数（单位：μg/m3）为0～50时，空气质量级别为一级，空气质量状况属于优；当空气污染指数为50～100时，空气质量级别为二级，空气质量状况属于良；当空气污染指数为100～150时，空气质量级别为三级，空气质量状况属于轻度污染；当空气污染指数为150～200时，空气质量级别为四级，空气质量状况属于中度污染；当空气污染指数为200～300时，空气质量级别为五级，空气质量状况属于重度污染；当空气污染指数为300以上时，空气质量级别为六级，空气质量状况属于严重污染．2015年8月某日某省x个监测点数据统计如下：| 空气污染指数 （单位：μg/m3） | [0，50] | （50，100] | （100，150][ | （150，200] |
| 监测点个数 | 15 | 40 | y | 10 |
（Ⅱ）在空气污染指数分别为50～100和150～200的监测点中，用分层抽样的方法抽取5个监测点，从中任意选取2个监测点，事件A“两个都为良”发生的概率是多少？
17．在区间[-2，1]任取两个实数x，y，则x+y＞0概率为（ ）
| A． | $\frac{2}{9}$ | B． | $\frac{4}{9}$ | C． | $\frac{1}{2}$ | D． | $\frac{7}{9}$ |