题目内容
抛物线y2=2ax(a>0)上的一点到焦点的距离为2a,则该点的纵坐标为________.
± a
a
分析:利用抛物线的性质将抛物线y2=2ax(a>0)上的一点到焦点的距离转化为它到其准线的距离即可.
解答:设抛物线y2=2ax(a>0)上的一点P(x0,y0)到焦点F(- ,0)的距离为2a,即|PF|=2a,
,0)的距离为2a,即|PF|=2a,
设P在抛物线y2=2ax(a>0)的准线上的射影为P′,
则|PP′|=|PF|=2a,又|PP′|=x0-(- )=x0+
)=x0+ ,
,
∴x0+ =2a,
=2a,
∴x0= .
.
∴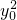 =2a•
=2a• =3a2,
=3a2,
∴y0=± a.
a.
故答案为:± a.
a.
点评:本题考查抛物线的性质,将抛物线y2=2ax(a>0)上的一点到焦点的距离转化为它到其准线的距离是关键,属于中档题.
 a
a分析:利用抛物线的性质将抛物线y2=2ax(a>0)上的一点到焦点的距离转化为它到其准线的距离即可.
解答:设抛物线y2=2ax(a>0)上的一点P(x0,y0)到焦点F(-
 ,0)的距离为2a,即|PF|=2a,
,0)的距离为2a,即|PF|=2a,设P在抛物线y2=2ax(a>0)的准线上的射影为P′,
则|PP′|=|PF|=2a,又|PP′|=x0-(-
 )=x0+
)=x0+ ,
,∴x0+
 =2a,
=2a,∴x0=
 .
.∴
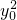 =2a•
=2a• =3a2,
=3a2,∴y0=±
 a.
a.故答案为:±
 a.
a.点评:本题考查抛物线的性质,将抛物线y2=2ax(a>0)上的一点到焦点的距离转化为它到其准线的距离是关键,属于中档题.

练习册系列答案
相关题目
 如图,已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,记直线AQ,BQ的斜率分别为k1,k2.
如图,已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,记直线AQ,BQ的斜率分别为k1,k2.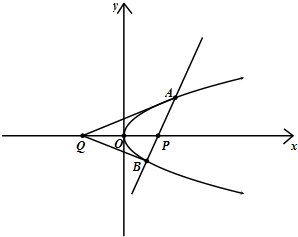 如图,已知动直线l经过点P(4,0),交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,设直线AQ,BQ的斜率分别为k1,k2.
如图,已知动直线l经过点P(4,0),交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,设直线AQ,BQ的斜率分别为k1,k2.