题目内容
若抛物线y2=2ax的准线经过双曲线
-y2=1的右焦点,则a=( )
| x2 |
| 3 |
分析:双曲线
-y2=1的右焦点坐标是(2,0),抛物线y2=2ax(a>0)的焦点坐标是(-
,0)由抛物线y2=ax(a>0)的焦点与双曲线
-y2=1的右焦点相同,知-
=2,求出a的值即可.
| x2 |
| 3 |
| a |
| 2 |
| x2 |
| 3 |
| a |
| 2 |
解答:解:双曲线
-y2=1的右焦点坐标是(2,0),
抛物线y2=2ax(a>0)的焦点坐标是(-
,0)
∵抛物线y2=ax(a>0)的焦点与双曲线
-y2=1的右焦点相同,
∴-
=2,a=-4,
故选B.
| x2 |
| 3 |
抛物线y2=2ax(a>0)的焦点坐标是(-
| a |
| 2 |
∵抛物线y2=ax(a>0)的焦点与双曲线
| x2 |
| 3 |
∴-
| a |
| 2 |
故选B.
点评:本题考查抛物线和双曲线的基本性质和应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
若抛物线y2=
与圆x2+y2-2ax+a2-1=0有且只有三个公共点,则a的取值范围是( )
| x |
| 2 |
| A、-1<a<1 | ||
B、
| ||
C、a=
| ||
| D、a=1 |
 如图,已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,记直线AQ,BQ的斜率分别为k1,k2.
如图,已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,记直线AQ,BQ的斜率分别为k1,k2.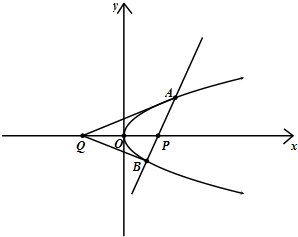 如图,已知动直线l经过点P(4,0),交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,设直线AQ,BQ的斜率分别为k1,k2.
如图,已知动直线l经过点P(4,0),交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,设直线AQ,BQ的斜率分别为k1,k2. 的右焦点,则a=
的右焦点,则a=