题目内容
已知点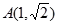 是离心率为
是离心率为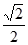 的椭圆
的椭圆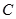 :
: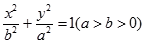 上的一点,斜率为
上的一点,斜率为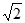 的直线
的直线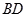 交椭圆
交椭圆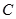 于
于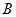 、
、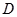 两点,且
两点,且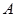 、
、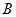 、
、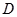 三点不重合.
三点不重合.
(1)求椭圆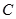 的方程;
的方程;
(2)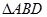 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由?
的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由?
(1)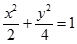 (2)
(2)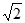
解析试题分析:解:(1)
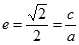 ,
, 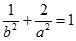 ,
,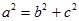
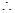
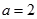 ,
,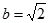 ,
,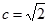
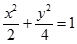
(2)设直线BD的方程为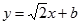
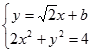
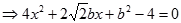
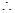
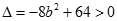
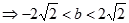
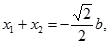 ----①
----① 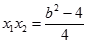 -----②
-----② ,
,
设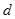 为点
为点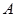 到直线BD:
到直线BD: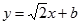 的距离,
的距离, 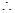
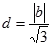
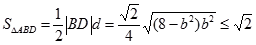 ,当且仅当
,当且仅当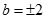 时取等号.
时取等号.
因为
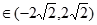 ,所以当
,所以当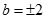 时,
时,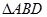 的面积最大,最大值为
的面积最大,最大值为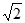
考点:椭圆的方程
点评:关于曲线的大题,第一问一般是求出曲线的方程,第二问常与直线结合起来,当涉及到最值时,常用到基本不等式。

练习册系列答案
相关题目
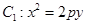 的焦点在抛物线
的焦点在抛物线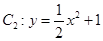 上.
上.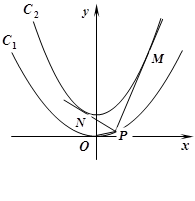
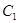 的方程及其准线方程;
的方程及其准线方程;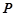 作抛物线
作抛物线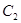 的两条切线
的两条切线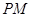 、
、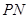 , 切点为
, 切点为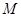 、
、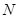 .若
.若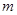 ,且
,且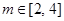 ,求
,求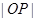 的取值范围.
的取值范围.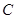 :
: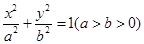 的右焦点为
的右焦点为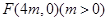 且
且 为常数,离心率为
为常数,离心率为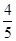 ,过焦点
,过焦点 、倾斜角为
、倾斜角为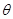 的直线
的直线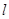 交椭圆
交椭圆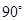 时,
时,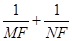 =
=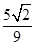 ,求实数
,求实数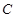 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,其左、右焦点分别为
轴上,其左、右焦点分别为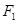 、
、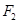 ,短轴长为
,短轴长为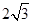 ,点
,点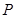 在椭圆
在椭圆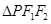 的周长为6.
的周长为6.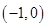 的直线与椭圆相交于A、B两点,试问在x轴上是否存在一个定点M使
的直线与椭圆相交于A、B两点,试问在x轴上是否存在一个定点M使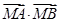 恒为定值?若存在求出该定值及点M的坐标,若不存在请说明理由.
恒为定值?若存在求出该定值及点M的坐标,若不存在请说明理由.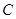 的极坐标方程为
的极坐标方程为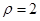 ,以极点为直角坐标系的原点,极轴为
,以极点为直角坐标系的原点,极轴为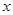 轴正半轴,两坐标系长度单位一致,建立平面直角坐标系.过圆
轴正半轴,两坐标系长度单位一致,建立平面直角坐标系.过圆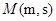 作平行于
作平行于 轴的直线
轴的直线 ,设
,设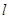 与
与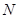 ,向量
,向量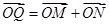 .
.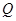 的轨迹方程;
的轨迹方程;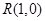 ,求
,求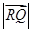 的最小值.
的最小值. ,
,
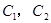 的方程为普通方程,并说明它们分别表示什么曲线?
的方程为普通方程,并说明它们分别表示什么曲线?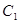 上的点P对应的参数为
上的点P对应的参数为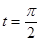 ,Q为
,Q为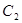 上的动点,求PQ的中点M到直线
上的动点,求PQ的中点M到直线 的距离的最小值
的距离的最小值 的离心率为
的离心率为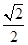 ,且经过点
,且经过点 .
. ,
, 两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且
两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且 .求△ABM的面积.
.求△ABM的面积.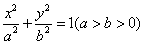 过点
过点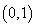 ,其长轴、焦距和短轴的长的平方依次成等差数列.直线
,其长轴、焦距和短轴的长的平方依次成等差数列.直线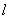 与
与 轴正半轴和
轴正半轴和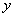 轴分别交于点
轴分别交于点 、
、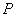 ,与椭圆分别交于点
,与椭圆分别交于点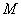 、
、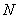 ,各点均不重合且满足
,各点均不重合且满足
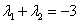 ,试证明:直线
,试证明:直线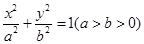 的离心率为
的离心率为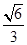 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为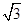 ,直线
,直线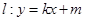 交椭圆于不同的两点
交椭圆于不同的两点 。
。 到直线
到直线 的距离为
的距离为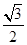 ,求
,求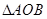 面积的最大值。
面积的最大值。