题目内容
9.函数$f(x)=\frac{1}{{{2^x}+1}}+a$为奇函数,则实数a=$-\frac{1}{2}$;函数f(x)在[1,3]上的值域为$[-\frac{7}{18},-\frac{1}{6}]$.分析 由定义知实数的奇函数满足f(0)=0求得a值;把求得的a值代入函数解析式,由x的范围求出2x+1的范围,然后求得函数值域.
解答 解:∵函数f(x)为奇函数,且函数$f(x)=\frac{1}{{{2^x}+1}}+a$的定义域为R,
∴f(0)=$\frac{1}{{2}^{0}+1}+a=\frac{1}{2}+a=0$,解得a=-$\frac{1}{2}$;
则$f(x)=\frac{1}{{2}^{x}+1}-\frac{1}{2}$,
当1≤x≤3时,3≤2x+1≤9,
∴$\frac{1}{9}≤\frac{1}{{2}^{x}+1}≤\frac{1}{3}$,
则$-\frac{7}{18}≤\frac{1}{{2}^{x}+1}-\frac{1}{2}≤-\frac{1}{6}$,
∴函数f(x)在[1,3]上的值域为$[-\frac{7}{18},-\frac{1}{6}]$.
故答案为:$-\frac{1}{2}$;$[-\frac{7}{18},-\frac{1}{6}]$.
点评 本题考查函数奇偶性的性质,考查函数值域的求法,考查不等式的性质,是中档题.

练习册系列答案
相关题目
16.一组数据x1,x2,…,x5的平均数为5,x${\;}_{1}^{2}$,x${\;}_{2}^{2}$,…,x${\;}_{5}^{2}$的平均数为33,则数据x1,x2,…,x5的方差为8.
14.函数f(x)=sin(ωx+φ)(ω>0,|φ|≤$\frac{π}{3}$)两条相邻的对称轴之间的距离为$\frac{π}{2}$,若其图象向右平移$\frac{π}{3}$个单位后得到的函数为奇函数,则函数f(x)( )
| A. | 关于点($\frac{π}{12}$,0)对称 | B. | 关于点($\frac{5π}{12}$,0)对称 | ||
| C. | 关于直线x=$\frac{5π}{12}$对称 | D. | 关于直线x=$\frac{π}{12}$对称 |
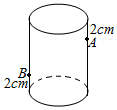 圆柱形玻璃杯高8cm,杯口周长为12cm,内壁距杯口2cm的点A处有一点蜜糖.A点正对面的外壁(不是A点的外壁)距杯底2cm的点B处有一小虫.若小虫沿杯壁爬向蜜糖饱食一顿,最少要爬多少10cm.(不计杯壁厚度与小虫的尺寸)
圆柱形玻璃杯高8cm,杯口周长为12cm,内壁距杯口2cm的点A处有一点蜜糖.A点正对面的外壁(不是A点的外壁)距杯底2cm的点B处有一小虫.若小虫沿杯壁爬向蜜糖饱食一顿,最少要爬多少10cm.(不计杯壁厚度与小虫的尺寸)
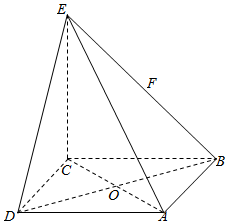 在四棱锥E-ABCD中,底面ABCD是边长为1的正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
在四棱锥E-ABCD中,底面ABCD是边长为1的正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.