题目内容
一次同时掷三颗骰子,至少有一颗出现“6”称为“状元秀”,则这样掷三次至少出现一次“状元秀”的概率为( )
A、1-(
| ||
B、1-(
| ||
C、1-[1-(
| ||
D、1-[1-(
|
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:根据三颗骰子每次都不出现6点的概率为(
)3,求出掷三次一直没有出现“状元秀”的概率,则用1减去此概率,即得所求.
| 5 |
| 6 |
解答:
解:每个筛子每次出现6点的概率为
,三颗骰子每次都不出现6点的概率为(
)3,
则这样掷三次一直没有出现“状元秀”的概率为 [(
)3]3=(
)9,
故这样掷三次至少出现一次“状元秀”的概率为 1-(
)9,
故选:A.
| 1 |
| 6 |
| 5 |
| 6 |
则这样掷三次一直没有出现“状元秀”的概率为 [(
| 5 |
| 6 |
| 5 |
| 6 |
故这样掷三次至少出现一次“状元秀”的概率为 1-(
| 5 |
| 5 |
故选:A.
点评:本题主要考查相互独立事件的概率乘法公式,所求的事件的概率与它的对立事件的概率之间的关系,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一个几何体的正视图和侧视图都是矩形,俯视图是一个圆(如图所示),该几何体的体积为( )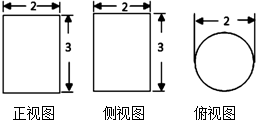

| A、π | B、2π | C、3π | D、4π |
要得到函数y=cosx的图象,只需要将函数y=cos(x-
)的图象( )
| π |
| 3 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
设(1-x)5(3+2x)9=a0(x+1)14+a1(x+1)13+…+a13(x+1)+a14,则a0+a1+a2+…+a13=( )
| A、39 |
| B、25-39 |
| C、25 |
| D、39-25 |
若不等式
≤μ≤
对任意的t∈(0,2]上恒成立,则μ的取值范围是( )
| t |
| t2+9 |
| ||
t+
|
A、[
| ||||||
B、[
| ||||||
C、[
| ||||||
D、[
|
复数
的实部和模分别为( )
| 2 |
| 1-i |
| A、1,2 | ||
| B、i,2 | ||
C、1,
| ||
D、i,
|
已知集合A={x|x2-2x≤0},B={x|y=log2(x-1)},则A∩B=( )
| A、{x|1≤x<2} |
| B、{x|1<x<2} |
| C、{x|1<x≤2} |
| D、{x|1≤x≤2} |