题目内容
如图,空间几何体ABCDEF中,四边形ABCD是菱形,直角梯形ADFE所在平面与面ABCD垂直,且AE⊥AD,EF∥AD,其中P,Q分别为棱BE,DF的中点.(1)求证:BD⊥CE;
(2)求证:PQ∥平面ABCD.
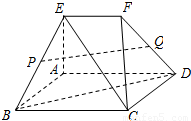
【答案】分析:(1)连接AC,在菱形ABCD中,AC⊥BD,由平面ADEF⊥平面ABCD,AE⊥AD,AE?平面ADEF,知AE⊥平面ABCD,由此能够证明BD⊥CE.
(2)取AE的中点G,连接PG,QG,在△ABE中,BP=PE,AG=GE,故PG∥BA,由PG?平面ABCD,BA?平面ABCD,知PG∥平面ABCD,由此能够证明PQ∥平面ABCD.
解答: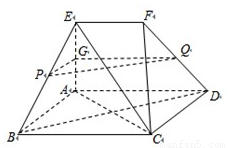 证明:(1)连接AC,在菱形ABCD中,AC⊥BD,
证明:(1)连接AC,在菱形ABCD中,AC⊥BD,
∵平面ADEF⊥平面ABCD,交线为AD,AE⊥AD,AE?平面ADEF,
∴AE⊥平面ABCD,
∵BD?平面ABCD,
∴AE⊥BD,
∵AC∩AE=A,∴BD⊥平面AEC,
∴BD⊥CE.
(2)取AE的中点G,连接PG,QG,
在△ABE中,BP=PE,AG=GE,∴PG∥BA,
∵PG?平面ABCD,BA?平面ABCD,
∴PG∥平面ABCD,
在梯形ADEF中,DQ=QF,AG=GE,
∴GQ∥AD,同理,GQ∥平面ABCD,
∵PG∩GQ=G,PG?平面PGQ,GQ?PQG,
∴平面PQG∥平面ABCD,
∵PQ?平面PQG,
∴PQ∥平面ABCD.
点评:本题考查直线与直线垂直的证明,考查直线与平面平行的证明.解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.
(2)取AE的中点G,连接PG,QG,在△ABE中,BP=PE,AG=GE,故PG∥BA,由PG?平面ABCD,BA?平面ABCD,知PG∥平面ABCD,由此能够证明PQ∥平面ABCD.
解答:
 证明:(1)连接AC,在菱形ABCD中,AC⊥BD,
证明:(1)连接AC,在菱形ABCD中,AC⊥BD,∵平面ADEF⊥平面ABCD,交线为AD,AE⊥AD,AE?平面ADEF,
∴AE⊥平面ABCD,
∵BD?平面ABCD,
∴AE⊥BD,
∵AC∩AE=A,∴BD⊥平面AEC,
∴BD⊥CE.
(2)取AE的中点G,连接PG,QG,
在△ABE中,BP=PE,AG=GE,∴PG∥BA,
∵PG?平面ABCD,BA?平面ABCD,
∴PG∥平面ABCD,
在梯形ADEF中,DQ=QF,AG=GE,
∴GQ∥AD,同理,GQ∥平面ABCD,
∵PG∩GQ=G,PG?平面PGQ,GQ?PQG,
∴平面PQG∥平面ABCD,
∵PQ?平面PQG,
∴PQ∥平面ABCD.
点评:本题考查直线与直线垂直的证明,考查直线与平面平行的证明.解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
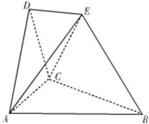 在如图所示的空间几何体中,△ABC,△ACD都是等边三角形,AE=CE,DE∥平面ABC,平面ACD⊥平面ABC.
在如图所示的空间几何体中,△ABC,△ACD都是等边三角形,AE=CE,DE∥平面ABC,平面ACD⊥平面ABC.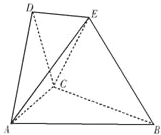 在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.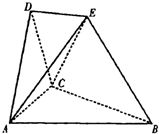 在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.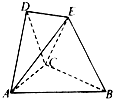 在如图所示的空间几何体中,平面ACD⊥平面ABC.BE和平面ABC所成的角为
在如图所示的空间几何体中,平面ACD⊥平面ABC.BE和平面ABC所成的角为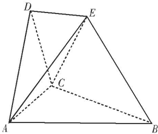 在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.