题目内容
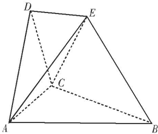 在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.(1)求证:DE∥平面ABC;
(2)求多面体ABCDE的体积.
分析:(1)取AC中点O,连接BO、DO,等边三角形△ACD中,DO⊥AC,结合面面垂直的性质,得D0⊥平面ABC.再过E作EF⊥平面ABC,可以证出四边形DEFO是平行四边形,得DE∥OF,结合线面平行的判定定理,证出DE∥平面ABC;
(2)三棱锥E-DAC中,可得DE是平面DAC上的高,三棱锥E-ABC中,EF是平面ABC上的高.最后用锥体体积公式,将三棱锥E-DAC的体积加上三棱锥E-ABC的体积,即可得到多面体ABCDE的体积.
(2)三棱锥E-DAC中,可得DE是平面DAC上的高,三棱锥E-ABC中,EF是平面ABC上的高.最后用锥体体积公式,将三棱锥E-DAC的体积加上三棱锥E-ABC的体积,即可得到多面体ABCDE的体积.
解答: 解:(1)取AC中点O,连接BO、DO,
解:(1)取AC中点O,连接BO、DO,
∵△ABC,△ACD都是边长为2的等边三角形,
∴BO⊥AC,DO⊥AC;
∵平面ACD⊥平面ABC,平面ACD∩平面ABC=AC
∴DO⊥平面ABC,
过E作EF⊥平面ABC,那么EF∥DO,
根据题意,点F落在BO上,易求得EF=DO=
,
所以四边形DEFO是平行四边形,得DE∥OF,
∵DE?平面ABC,OF?平面ABC,∴DE∥平面ABC…(6分)
(2)∵平面ACD⊥平面ABC,平面ACD∩平面ABC=AC,OB⊥AC,
∴OB⊥平面ACD;
又∵DE∥OB,∴DE⊥平面DAC,
∴三棱锥E-DAC的体积:V1=
S△BAC•DE=
•
•(
-1)=
又∵三棱锥E-ABC的体积V2=
S△ABC•EF=
•
•
=1
∴多面体DE-ABC的体积为V=V1+V2=
…(12分)
 解:(1)取AC中点O,连接BO、DO,
解:(1)取AC中点O,连接BO、DO,∵△ABC,△ACD都是边长为2的等边三角形,
∴BO⊥AC,DO⊥AC;
∵平面ACD⊥平面ABC,平面ACD∩平面ABC=AC
∴DO⊥平面ABC,
过E作EF⊥平面ABC,那么EF∥DO,
根据题意,点F落在BO上,易求得EF=DO=
| 3 |
所以四边形DEFO是平行四边形,得DE∥OF,
∵DE?平面ABC,OF?平面ABC,∴DE∥平面ABC…(6分)
(2)∵平面ACD⊥平面ABC,平面ACD∩平面ABC=AC,OB⊥AC,
∴OB⊥平面ACD;
又∵DE∥OB,∴DE⊥平面DAC,
∴三棱锥E-DAC的体积:V1=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
3-
| ||
| 3 |
又∵三棱锥E-ABC的体积V2=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
∴多面体DE-ABC的体积为V=V1+V2=
6-
| ||
| 3 |
点评:本题给出两个三棱锥拼接成多面体,求证线面平行并且求它的体积,着重考查了面面垂直的性质、线面平行的判定和锥体体积公式等知识,属于中档题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
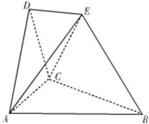 在如图所示的空间几何体中,△ABC,△ACD都是等边三角形,AE=CE,DE∥平面ABC,平面ACD⊥平面ABC.
在如图所示的空间几何体中,△ABC,△ACD都是等边三角形,AE=CE,DE∥平面ABC,平面ACD⊥平面ABC.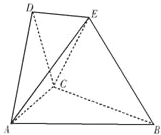 在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.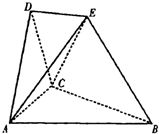 在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.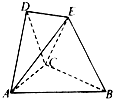 在如图所示的空间几何体中,平面ACD⊥平面ABC.BE和平面ABC所成的角为
在如图所示的空间几何体中,平面ACD⊥平面ABC.BE和平面ABC所成的角为