题目内容
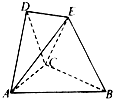 在如图所示的空间几何体中,平面ACD⊥平面ABC.BE和平面ABC所成的角为
在如图所示的空间几何体中,平面ACD⊥平面ABC.BE和平面ABC所成的角为| π |
| 3 |
| 3 |
(1)求证:DE∥平面ABC;
(2)求二面角A-BE-C的余弦值.
分析:(1)取AC中点O,连接BO、DO,等边三角形△ACD中,DO⊥AC,结合面面垂直的性质,得D0⊥平面ABC.再过E作EF⊥平面ABC,可以证出四边形DEFO是平行四边形,得DE∥OF,结合线面平行的判定定理,证出DE∥平面ABC;
(2)以O为坐标原点,OA,OB,OD分别为x,y,z轴方向建立空间坐标系,分别求出平面ABE和CBE的法向量,代入向量夹角公式,可得答案.
(2)以O为坐标原点,OA,OB,OD分别为x,y,z轴方向建立空间坐标系,分别求出平面ABE和CBE的法向量,代入向量夹角公式,可得答案.
解答: 证明:(1)取AC中点O,连接BO、DO,
证明:(1)取AC中点O,连接BO、DO,
∵△ABC,△ACD都是边长为2的等边三角形,
∴BO⊥AC,DO⊥AC;
∵平面ACD⊥平面ABC,平面ACD∩平面ABC=AC
∴DO⊥平面ABC,
过E作EF⊥平面ABC,那么EF∥DO,
根据题意,点F落在BO上,易求得EF=DO=
,
所以四边形DEFO是平行四边形,得DE∥OF,
∵DE?平面ABC,OF?平面ABC,
∴DE∥平面ABC
(2)以O为坐标原点,OA,OB,OD分别为x,y,z轴方向建立空间坐标系,
则A(1,0,0),B(0,
,0),C(-1,0,0),D(0,0,
),E(0,
-1,
)
则
=(0,-1,
),
=(-1,
,0),
=(1,
,0),
设平面ABE的法向量为
=(x,y,z)
则
,即
令y=
,可得
=(3,
,1)
设平面ACE的法向量为
=(x,y,z)
则
,即
令y=
,可得
=(-3,
,1)
设锐二面角A-BE-C的平面角为θ
则cosθ=
=
=
,即二面角A-BE-C的余弦值为
 证明:(1)取AC中点O,连接BO、DO,
证明:(1)取AC中点O,连接BO、DO,∵△ABC,△ACD都是边长为2的等边三角形,
∴BO⊥AC,DO⊥AC;
∵平面ACD⊥平面ABC,平面ACD∩平面ABC=AC
∴DO⊥平面ABC,
过E作EF⊥平面ABC,那么EF∥DO,
根据题意,点F落在BO上,易求得EF=DO=
| 3 |
所以四边形DEFO是平行四边形,得DE∥OF,
∵DE?平面ABC,OF?平面ABC,
∴DE∥平面ABC
(2)以O为坐标原点,OA,OB,OD分别为x,y,z轴方向建立空间坐标系,
则A(1,0,0),B(0,
| 3 |
| 3 |
| 3 |
| 3 |
则
| BE |
| 3 |
| AB |
| 3 |
| CB |
| 3 |
设平面ABE的法向量为
| m |
则
|
|
令y=
| 3 |
| m |
| 3 |
设平面ACE的法向量为
| n |
则
|
|
令y=
| 3 |
| n |
| 3 |
设锐二面角A-BE-C的平面角为θ
则cosθ=
| ||||
|
|
|
| ||||
|
|
| 5 |
| 13 |
| 5 |
| 13 |
点评:本题考查的知识点是直线与平面平行的判定,二面角的平面角的求法,建立空间坐标系,将二面角问题转化为向量夹角问题是解答的关键.

练习册系列答案
相关题目
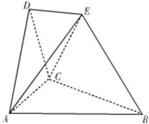 在如图所示的空间几何体中,△ABC,△ACD都是等边三角形,AE=CE,DE∥平面ABC,平面ACD⊥平面ABC.
在如图所示的空间几何体中,△ABC,△ACD都是等边三角形,AE=CE,DE∥平面ABC,平面ACD⊥平面ABC.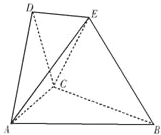 在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.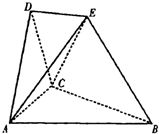 在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.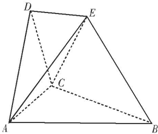 在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.