题目内容
设函数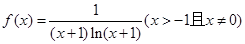 .
.
⑴求函数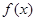 的单调区间;
的单调区间;
⑵求函数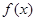 的值域;
的值域;
⑶已知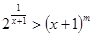 对
对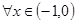 恒成立,求实数
恒成立,求实数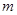 的取值范围.
的取值范围.
【答案】
(1)详见解析;(2)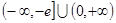 ;(3)
;(3)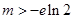 .
.
【解析】
试题分析:(1)判断函数的单调区间,一般利用其导数的符号判断,使导函数为正的区间是增区间,使函数为负的区间是减区间;(2)函数的值域则可利用(1)中得到的函数的单调性进行求解;(3)恒成立问题则常用分离参数的方法,转化为求函数的最值问题,而求函数的最值则仍可利用导数去判断函数的单调性.
试题解析:⑴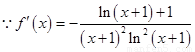 ,由
,由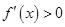 解得
解得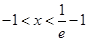 ,
,
由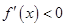 解得,
解得,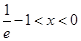 或
或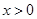 ,
,
故函数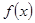 的单调递增区间是
的单调递增区间是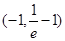 ,单调递减区间是
,单调递减区间是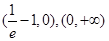 .
.
4分
⑵当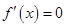 时,解得
时,解得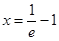 ,由⑴可知函数
,由⑴可知函数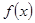 在
在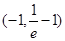 上递增,在
上递增,在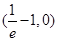 上递减,
上递减,
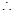 在区间
在区间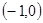 上,
上,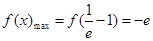 ;
;
在区间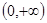 上,
上,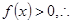 函数
函数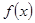 的值域为
的值域为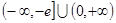 .
8分
.
8分
⑶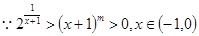 ,两边取自然对数得
,两边取自然对数得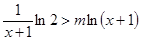 ,
,
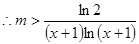 对
对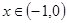 恒成立,则
恒成立,则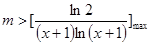 ,
,
由⑵可知当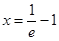 时,
时,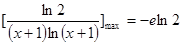 ,
,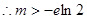 . 12分
. 12分
考点:函数与导数、函数的单调性、不等式恒成立.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 .
. 的单调区间;
的单调区间; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.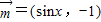 ,
,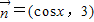 .
.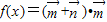 ,求函数f(x)的单调递增区间;
,求函数f(x)的单调递增区间;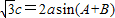 ,对于(1)中的函数f(x),求
,对于(1)中的函数f(x),求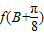 的取值范围.
的取值范围.

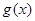 =
=
 ,求证:当
,求证:当 时,有
时,有 成立
成立 .
. 的单调区间;
的单调区间; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. .
. 的单调区间;
的单调区间; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.