题目内容
已知向量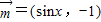 ,
,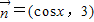 .
.(1)设函数
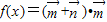 ,求函数f(x)的单调递增区间;
,求函数f(x)的单调递增区间;(2)已知在锐角△ABC中,a,b,c分别为角A,B,C的对边,
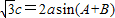 ,对于(1)中的函数f(x),求
,对于(1)中的函数f(x),求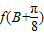 的取值范围.
的取值范围.
【答案】分析:(1)由向量的坐标运算、数量积运算,以及倍角公式、两角差的正弦公式化简解析式,再由正弦函数的增区间得: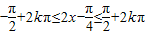 ,求出x的范围表示成区间的形式即可;
,求出x的范围表示成区间的形式即可;
(2)由正弦定理对所给的式子进行转化: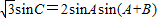 ,再由内角和定理和特殊角的正弦求出A,再由内角和定理表示出C,根据内角是锐角求出B的范围,再化简
,再由内角和定理和特殊角的正弦求出A,再由内角和定理表示出C,根据内角是锐角求出B的范围,再化简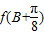 ,求出2B的范围,根据正弦函数的性质求出
,求出2B的范围,根据正弦函数的性质求出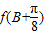 的范围.
的范围.
解答:解:(1)由题意得,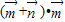 =(sinx+cosx,2)•(sinx,-1)
=(sinx+cosx,2)•(sinx,-1)
=sin2x+sinxcosx-2=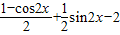
=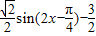 ,
,
则f(x)=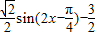 ,
,
由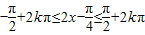 (k∈z)得,
(k∈z)得,
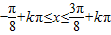 (k∈z),
(k∈z),
∴f(x)的单调递增区间是[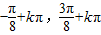 ](k∈z),
](k∈z),
(2)∵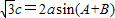
∴由正弦定理得,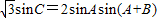 ,
,
∵A+B+C=π,∴A+B=π-C代入上式得,sinA=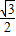 ,
,
∵△ABC是锐角三角形,∴A=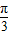 ,
,
∴c=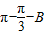 =
=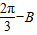 ,
,
则0<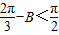 ,且B是锐角,
,且B是锐角,
解得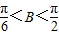 ①,
①,
由(1)得,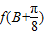 =
=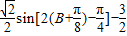
=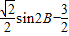 ,
,
由①得,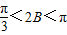 ,
,
当2B=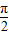 时,
时,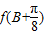 取得最大值是
取得最大值是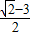 ,
,
当2B=π时,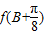 取得最小值是
取得最小值是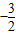 ,
,
故所求的取值范围是(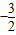 ,
,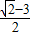 ].
].
点评:本题考查了正弦函数的单调性、最值,正弦定理和内角和定理,向量的坐标运算、数量积运算,以及倍角公式、两角差的正弦公式的应用,关键是熟练掌握公式并会运用,考查整体思考和计算能力,是向量与三角函数结合题,常考的一种题型.
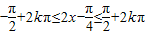 ,求出x的范围表示成区间的形式即可;
,求出x的范围表示成区间的形式即可;(2)由正弦定理对所给的式子进行转化:
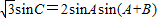 ,再由内角和定理和特殊角的正弦求出A,再由内角和定理表示出C,根据内角是锐角求出B的范围,再化简
,再由内角和定理和特殊角的正弦求出A,再由内角和定理表示出C,根据内角是锐角求出B的范围,再化简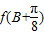 ,求出2B的范围,根据正弦函数的性质求出
,求出2B的范围,根据正弦函数的性质求出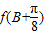 的范围.
的范围.解答:解:(1)由题意得,
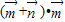 =(sinx+cosx,2)•(sinx,-1)
=(sinx+cosx,2)•(sinx,-1)=sin2x+sinxcosx-2=
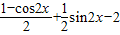
=
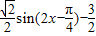 ,
,则f(x)=
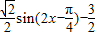 ,
,由
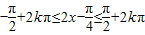 (k∈z)得,
(k∈z)得,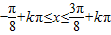 (k∈z),
(k∈z),∴f(x)的单调递增区间是[
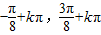 ](k∈z),
](k∈z),(2)∵
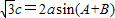
∴由正弦定理得,
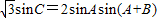 ,
,∵A+B+C=π,∴A+B=π-C代入上式得,sinA=
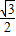 ,
,∵△ABC是锐角三角形,∴A=
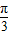 ,
,∴c=
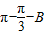 =
=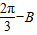 ,
,则0<
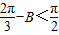 ,且B是锐角,
,且B是锐角,解得
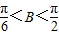 ①,
①,由(1)得,
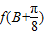 =
=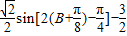
=
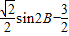 ,
,由①得,
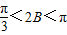 ,
,当2B=
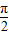 时,
时,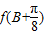 取得最大值是
取得最大值是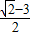 ,
,当2B=π时,
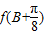 取得最小值是
取得最小值是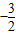 ,
,故所求的取值范围是(
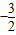 ,
,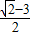 ].
].点评:本题考查了正弦函数的单调性、最值,正弦定理和内角和定理,向量的坐标运算、数量积运算,以及倍角公式、两角差的正弦公式的应用,关键是熟练掌握公式并会运用,考查整体思考和计算能力,是向量与三角函数结合题,常考的一种题型.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 ,
, ,
,
 ,求
,求 ;
; 与
与 垂直,求
垂直,求 的值;
的值; 方向上的投影.
方向上的投影. ,
, ,
, ,求
,求 ;
; 与
与 垂直,求
垂直,求 的值;
的值; 方向上的投影.
方向上的投影.