题目内容
设函数

(1)求函数 的单调区间
的单调区间
(2)设函数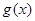 =
=

 ,求证:当
,求证:当 时,有
时,有 成立
成立
【答案】
(1) 当 时,
时, >0,所以
>0,所以 为单调递增区间 4分
为单调递增区间 4分
当 时,由
时,由 >0得
>0得 ,即
,即 为其单调增区间,由
为其单调增区间,由 <0得,即
<0得,即 为其减区间
为其减区间
(2)构造函数由函数 =
=

 =
= ,借助于导数来判定单调性,进而得到证明。
,借助于导数来判定单调性,进而得到证明。
【解析】
试题分析:(1)解: 定义域为
定义域为 1分
1分
 =
= =
= 2分
2分
当 时,
时, >0,所以
>0,所以 为单调递增区间 4分
为单调递增区间 4分
当 时,由
时,由 >0得
>0得 ,即
,即 为其单调增区间
为其单调增区间
由 <0得,即
<0得,即 为其减区间 7分
为其减区间 7分
(2)证明:由函数 =
=

 =
= 得
得
 =
= 9分
9分
由(1)知,当 =1时,
=1时,


即不等式 成立
11分
成立
11分
所以当 时,
时, =
=


=
 0
0
即 在
在 上单调递减,
上单调递减,
从而

 满足题意
14分
满足题意
14分
考点:导数的运用
点评:解决的关键是根据导数的符号判定单调性,以及函数的最值得到证明,属于基础题。

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 .
. ABC的三个内角,若cosB=
ABC的三个内角,若cosB= ,
, ,求sinA.
,求sinA. .
. 的单调区间;
的单调区间; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. .
.  的单调区间;
的单调区间; 时,是否存在整数
时,是否存在整数 ,使不等式
,使不等式 恒成立?若
恒成立?若 的方程
的方程 在
在 上恰有两个相异实根,求实数
上恰有两个相异实根,求实数 的取值范围。
的取值范围。