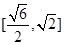题目内容
若函数 的图象在
的图象在 处的切线
处的切线 与圆
与圆 相离,则点
相离,则点 与圆C的位置关系是 ( )
与圆C的位置关系是 ( )
| A.点在圆外 | B.点在圆内 | C.点在圆上 | D.不能确定 |
B
解析试题分析:∵ ,∴
,∴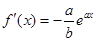 ,∴在x=0处切线斜率为
,∴在x=0处切线斜率为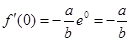 ,∴切线l为y-
,∴切线l为y-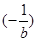 =
=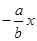 ,即ax+by+1="0," ∵
,即ax+by+1="0," ∵ 与圆
与圆 相离, ∴
相离, ∴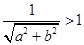 , ∴
, ∴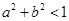 , ∴点P(a,b)在圆
, ∴点P(a,b)在圆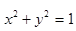 的内部,故选B
的内部,故选B
考点:本题考查了导数的运用及直线与圆的位置关系
点评: 在
在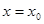 处导数
处导数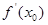 即为
即为 所表示曲线在
所表示曲线在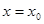 处切线的斜率,即
处切线的斜率,即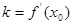 ,则切线方程为:
,则切线方程为: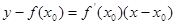

练习册系列答案
相关题目
若直线 与圆
与圆 相切,则
相切,则 的值为( )
的值为( )
A. | B. | C. | D. 或 或 |
两圆相交于点A(1,3)、B(m,-1),两圆的圆心均在直线x-y+c=0上,则m+c的值为( )
| A.3 | B.2 | C.0 | D.-1 |
若直线x-y=2被圆(x-a)2+y2=4所截得的弦长为2 ,则实数a的值为
,则实数a的值为
A.-1或 | B.1或3 | C.-2或6 | D.0或4 |
若实数 满足
满足 ,
, 的取值范围为( ).
的取值范围为( ).
A. | B. | C. | D. |
过点 作圆
作圆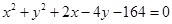 的弦,其中弦长为整数的共有( )
的弦,其中弦长为整数的共有( )
| A.16条 | B.17条 | C.32条 | D.34条 |
直线 截圆
截圆 所得劣弧所对的圆心角是
所得劣弧所对的圆心角是
A.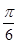 | B. |
C. | D. |
设两圆C1、C2都和两坐标轴相切,且都过点(4,1),则两圆心的距离|C1C2|=( )
| A.4 | B.4 | C.8 | D.8 |
 (a>0,b>0)的左右焦点分别为F1,F2,P为双曲线上任一点,已知|
(a>0,b>0)的左右焦点分别为F1,F2,P为双曲线上任一点,已知| |·|
|·| |的最小值为m.当
|的最小值为m.当 ≤m≤
≤m≤ 时,其中c=
时,其中c= ,则双曲线的离心率e的取值范围是 ( )
,则双曲线的离心率e的取值范围是 ( )