题目内容
双曲线 (a>0,b>0)的左右焦点分别为F1,F2,P为双曲线上任一点,已知|
(a>0,b>0)的左右焦点分别为F1,F2,P为双曲线上任一点,已知| |·|
|·| |的最小值为m.当
|的最小值为m.当 ≤m≤
≤m≤ 时,其中c=
时,其中c= ,则双曲线的离心率e的取值范围是 ( )
,则双曲线的离心率e的取值范围是 ( )
A. | B. | C. | D.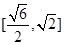 |
D
解析试题分析:根据题意,由于双曲线 (a>0,b>0)的左右焦点分别为F1,F2,P为双曲线上任一点,则根据焦半径的定义得到|
(a>0,b>0)的左右焦点分别为F1,F2,P为双曲线上任一点,则根据焦半径的定义得到| |·|
|·| |=
|= ,根据
,根据 ≤m≤
≤m≤ ,可知双曲线的离心率e的取值范围是
,可知双曲线的离心率e的取值范围是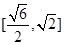 ,选D.
,选D.
考点:双曲线的性质
点评:本题考查双曲线的性质和应用,解题时要认真审题,注意焦半径公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
圆 截直线
截直线 所得弦长是( )
所得弦长是( )
| A.2 | B.1 | C. | D. |
直线 与圆
与圆 相交于
相交于 ,
, 两点,且
两点,且 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
下列满足“与直线 平行,且与圆
平行,且与圆 相切”的是( )
相切”的是( )
A.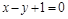 | B. |
C. | D. |
已知点 内任意一点,点
内任意一点,点 是圆上任意一点,则实数
是圆上任意一点,则实数 ( )
( )
| A.一定是负数 | B.一定等于0 |
| C.一定是正数 | D.可能为正数也可能为负数 |
已知圆O: ,直线
,直线 过点
过点 ,且与直线OP垂直,则直线
,且与直线OP垂直,则直线 的方程为( )
的方程为( )
A. | B. | C. | D. |
若函数 的图象在
的图象在 处的切线
处的切线 与圆
与圆 相离,则点
相离,则点 与圆C的位置关系是 ( )
与圆C的位置关系是 ( )
| A.点在圆外 | B.点在圆内 | C.点在圆上 | D.不能确定 |
过点A(1,-1),B(-1,1),且圆心在直线x+y-2=0上的圆的方程是( )
| A.(x-3)2+(y+1)2=4 | B.(x-1)2+(y-1)2=4 |
| C.(x+3)2+(y-1)2=4 | D.(x+1)2+(y+1)2=4 |
 中,圆
中,圆 的方程为
的方程为 ,若直线
,若直线 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆 的取值范围是( )
的取值范围是( )
 或
或
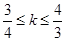
 或
或