题目内容
已知:a,b∈R+且
+
=2,则a+b的最小值是
+
+
.
| 1 |
| a |
| 2 |
| b |
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
分析:由题设条件知a+b=(a+b)×
(
+
)=
+
(
+
),由此利用均值不等式可得到a+b的最小值.
| 1 |
| 2 |
| 1 |
| a |
| 2 |
| b |
| 3 |
| 2 |
| 1 |
| 2 |
| b |
| a |
| 2a |
| b |
解答:解:∵a,b∈R+,
+
=2,
∴a+b=(a+b)×
(
+
)=
+
(
+
)≥
+
×2
=
+
,
当且仅当
=
,即a=
,b=
时,等号成立.
故a+b的最小值为
+
故答案为
+
| 1 |
| a |
| 2 |
| b |
∴a+b=(a+b)×
| 1 |
| 2 |
| 1 |
| a |
| 2 |
| b |
| 3 |
| 2 |
| 1 |
| 2 |
| b |
| a |
| 2a |
| b |
| 3 |
| 2 |
| 1 |
| 2 |
|
| 3 |
| 2 |
| 2 |
当且仅当
| b |
| a |
| 2a |
| b |
1+
| ||
| 2 |
| ||
| 2 |
故a+b的最小值为
| 3 |
| 2 |
| 2 |
故答案为
| 3 |
| 2 |
| 2 |
点评:本题考查基本不等式的应用,注意检验等号成立的条件,式子的变形是解题的关键.

练习册系列答案
相关题目
 ,其中
,其中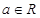 ,b∈R且b≠0。
,b∈R且b≠0。 的单调区间;
的单调区间; 没有实根,求a的取值范围;
没有实根,求a的取值范围; ,其中
,其中 .
.
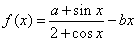 (a、b∈R),
(a、b∈R),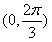 为增函数,
为增函数,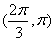 为减函数,若存在,求出b的值,若不存在,请说明理由;
为减函数,若存在,求出b的值,若不存在,请说明理由;