题目内容
已知函数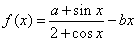 (a、b∈R),
(a、b∈R),
(Ⅰ)若f(x)在R上存在最大值与最小值,且其最大值与最小值的和为2680,试求a 和b的值;
(Ⅱ)若f(x)为奇函数:(1)是否存在实数b,使得f(x)在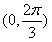 为增函数,
为增函数,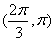 为减函数,若存在,求出b的值,若不存在,请说明理由;
为减函数,若存在,求出b的值,若不存在,请说明理由;
(2)如果当x≥0时,都有f(x)≤0恒成立,试求b的取值范围。
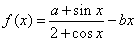 (a、b∈R),
(a、b∈R),(Ⅰ)若f(x)在R上存在最大值与最小值,且其最大值与最小值的和为2680,试求a 和b的值;
(Ⅱ)若f(x)为奇函数:(1)是否存在实数b,使得f(x)在
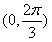 为增函数,
为增函数,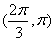 为减函数,若存在,求出b的值,若不存在,请说明理由;
为减函数,若存在,求出b的值,若不存在,请说明理由;(2)如果当x≥0时,都有f(x)≤0恒成立,试求b的取值范围。
解:(Ⅰ)∵f(x)在x∈R上存在最大值和最小值,
∴b=0(否则f(x)值域为R),
∴

 ,
,
又 ,
,
由题意有 , ∴a=2010;
, ∴a=2010;
(Ⅱ)若f(x)为奇函数,∵x∈R,∴f(0)=0,∴a=0,
∴ ,
, ,
,
(1)若 ,使f(x)在(0,
,使f(x)在(0, )上递增,在(
)上递增,在( ,π)上递减,
,π)上递减,
则 ,∴b=0,
,∴b=0,
这时 ,
,
当 时,
时, ,f(x)递增;
,f(x)递增;
当 时,
时, ,f(x)递减。
,f(x)递减。
(2) ,
,
△= ,
,
若△≤0,即 ,则
,则 对
对 恒成立,这时f(x)在
恒成立,这时f(x)在 上递减,
上递减,
∴ 。
。
若b<0,则当x≥0时, ,
, ,
,
 不可能恒小于等于0;
不可能恒小于等于0;
若b=0,则 不合题意,
不合题意,
若 ,则
,则 ,
, ,
,
所以, ,使
,使 ,
,

综上所述, 。
。
∴b=0(否则f(x)值域为R),
∴


 ,
,又
 ,
,由题意有
 , ∴a=2010;
, ∴a=2010; (Ⅱ)若f(x)为奇函数,∵x∈R,∴f(0)=0,∴a=0,
∴
 ,
, ,
, (1)若
 ,使f(x)在(0,
,使f(x)在(0, )上递增,在(
)上递增,在( ,π)上递减,
,π)上递减,则
 ,∴b=0,
,∴b=0,这时
 ,
,当
 时,
时, ,f(x)递增;
,f(x)递增; 当
 时,
时, ,f(x)递减。
,f(x)递减。(2)
 ,
,△=
 ,
,若△≤0,即
 ,则
,则 对
对 恒成立,这时f(x)在
恒成立,这时f(x)在 上递减,
上递减,∴
 。
。若b<0,则当x≥0时,
 ,
, 若b=0,则
 不合题意,
不合题意,若
所以,

综上所述,

练习册系列答案
相关题目
 (a,b为常数),在R上连续,则a的值是
(a,b为常数),在R上连续,则a的值是 ,其中
,其中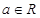 ,b∈R且b≠0。
,b∈R且b≠0。 的单调区间;
的单调区间; 没有实根,求a的取值范围;
没有实根,求a的取值范围; ,其中
,其中 .
.