题目内容
(本大题满分14分)
已知函数 ,其中
,其中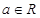 ,b∈R且b≠0。
,b∈R且b≠0。
(1)求 的单调区间;
的单调区间;
(2)当b=1时,若方程 没有实根,求a的取值范围;
没有实根,求a的取值范围;
(3)证明: ,其中
,其中 .
.
【答案】
解:(1)由题意可知: ,b≠0时,
,b≠0时,
令 ,得
,得 ,
(1分)
,
(1分)
则①b>0,当 时,
时, ,
, 单调递减;
单调递减;
当 时,
时, ,
, 单调递增
(3分)②b<0,当
单调递增
(3分)②b<0,当 时,
时, ,
, 单调递增;
单调递增;
当 时,
时, ,
, 单调递减
(5分)
单调递减
(5分)
(2)由(1)可得 在
在 处取得极小值,且
处取得极小值,且 没有实根,
(7分)
没有实根,
(7分)
则 ,即
,即 ,解得:
,解得: (8分)
(8分)
(3)方法1:由(2)得,令 ,
, 成立,
成立,
则 ,
, 恒成立
(10分)
恒成立
(10分)
故



 ,即得证。
(14分)
,即得证。
(14分)
方法2:数学归纳法
(1)
当 时,
时, 成立;
成立;
(2)
当 时,
时, 成立,
成立,
当 时,
时,

同理令 ,
, ,即
,即 ,
(10分)
,
(10分)
则 ,
(12分)
,
(12分)
故 ,
,
即 对
对 也成立,
也成立,
综合(1)(2)得: ,
, 恒成立。 (14分)
恒成立。 (14分)
【解析】略

练习册系列答案
相关题目
 如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用
如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,
, ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于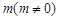 .
. 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 时,过点
时,过点 的直线
的直线 交曲线
交曲线 于
于 两点,设点
两点,设点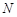 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合).求证直线
不重合).求证直线 与
与 ,
, ,当
,当 为何值时,
为何值时,
 与
与
 和
和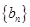 满足:
满足: ,
, ,
,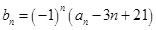 ,其中
,其中 为实数,
为实数, 为正整数.
为正整数. 时,数列
时,数列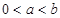 (
( 为实常数),
为实常数),  为数列
为数列 ?若存在,求
?若存在,求 过椭圆C:
过椭圆C: 的右焦点F,
的右焦点F, 上的射影依次为点D、E.
上的射影依次为点D、E. 
 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程; 为x轴上一点;
为x轴上一点;