题目内容
1.已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别是点F1,F2,上、下顶点分别为A,B,其离心率e=$\frac{1}{2}$,点P为椭圆上的一个动点,当点P与点A重合时,△PF1F2的内切圆面积为$\frac{4π}{3}$.(I)求a,b的值;
(Ⅱ)当点P是椭圆上异于顶点的任意一点,直线AP,BP分别交x轴于两点M,N,证明:|$\overrightarrow{OM}$|•|$\overrightarrow{ON}$|为定值.
分析 (I)由当点P与点A重合时,△PF1F2的内切圆面积为$\frac{4π}{3}$.设内切圆的半径为r,则πr2=$\frac{4π}{3}$,解得r.利用$\frac{1}{2}r×(2a+2c)$=$\frac{1}{2}×2c×b$,又$\frac{c}{a}$=$\frac{1}{2}$,a2=b2+c2,联立解出即可得出.
(II)由(I)可得椭圆的方程为:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}$=1.可得A(0,2$\sqrt{3}$),B(0,-2$\sqrt{3}$),设P$(4cosθ,2\sqrt{3}sinθ)$.(θ∈[0,2π)).则直线AP的方程为:y=$\frac{\sqrt{3}sinθ-\sqrt{3}}{2cosθ}$x+2$\sqrt{3}$,可得M.同理可得B,即可证明|$\overrightarrow{OM}$|•|$\overrightarrow{ON}$|为定值.
解答 (I)解:∵当点P与点A重合时,△PF1F2的内切圆面积为$\frac{4π}{3}$.
设内切圆的半径为r,则πr2=$\frac{4π}{3}$,解得r=$\frac{2\sqrt{3}}{3}$.
∴$\frac{1}{2}r×(2a+2c)$=$\frac{1}{2}×2c×b$,化为:2(a+c)=$\sqrt{3}$bc,
又$\frac{c}{a}$=$\frac{1}{2}$,a2=b2+c2,联立解得a=4,b=2$\sqrt{3}$,c=2.
(II)证明:由(I)可得椭圆的方程为:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}$=1.
∴A(0,2$\sqrt{3}$),B(0,-2$\sqrt{3}$),设P$(4cosθ,2\sqrt{3}sinθ)$.(θ∈[0,2π),$θ≠\frac{π}{2}$,$\frac{3π}{2}$).
则直线AP的方程为:y=$\frac{\sqrt{3}sinθ-\sqrt{3}}{2cosθ}$x+2$\sqrt{3}$,可得M$(\frac{4cosθ}{1-sinθ},0)$.$(θ≠\frac{π}{2})$
直线BP的方程为:y=$\frac{\sqrt{3}sinθ+\sqrt{3}}{2cosθ}$x-2$\sqrt{3}$,可得N$(\frac{4cosθ}{sinθ+1},0)$.$(θ≠\frac{3π}{2})$.
∴|$\overrightarrow{OM}$|•|$\overrightarrow{ON}$|=$\frac{16co{s}^{2}θ}{1-si{n}^{2}θ}$=16为定值.
点评 本题考查了椭圆的标准方程及其性质、三角形内切圆的面积与三角形的面积计算公式、直线的方程,考查了推理能力与计算能力,属于难题.

 期末集结号系列答案
期末集结号系列答案| A. | 1 | B. | -1 | C. | -2或1 | D. | -1或-2 |
| A. | 若α⊥β,则l∥m | B. | 若α⊥β,则l⊥m | C. | 若l⊥m,则α∥β | D. | 若l∥m,则α⊥β |
| A. | ${∫}_{0}^{1}$$\frac{1}{x}$dx | B. | ${∫}_{0}^{1}$xpdx | C. | ${∫}_{0}^{1}$($\frac{1}{x}$)pdx | D. | ${∫}_{0}^{1}$($\frac{x}{n}$)pdx |
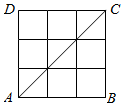 如图,ABCD为边长为3的正方形,把各边三等分后,共有16个交点,从中选取两个交点作为向量,则与$\overrightarrow{AC}$平行且长度为2$\sqrt{2}$的向量个数有8个.
如图,ABCD为边长为3的正方形,把各边三等分后,共有16个交点,从中选取两个交点作为向量,则与$\overrightarrow{AC}$平行且长度为2$\sqrt{2}$的向量个数有8个.